Jia Li
James Z. Wang
Gio Wiederhold
Department of Computer Science
Stanford University
{jiali,wangz,gio}@db.stanford.edu
(www-db.stanford.edu/IMAGE)
Content-based image retrieval using region segmentation has been an active research area. We present IRM (Integrated Region Matching), a novel similarity measure for region-based image similarity comparison. The targeted image retrieval systems represent an image by a set of regions, roughly corresponding to objects, which are characterized by features reflecting color, texture, shape, and location properties. The IRM measure for evaluating overall similarity between images incorporates properties of all the regions in the images by a region-matching scheme. Compared with retrieval based on individual regions, the overall similarity approach reduces the influence of inaccurate segmentation, helps to clarify the semantics of a particular region, and enables a simple querying interface for region-based image retrieval systems. The IRM has been implemented as a part of our experimental SIMPLIcity image retrieval system. The application to a database of about 200,000 general-purpose images shows exceptional robustness to image alterations such as intensity variation, sharpness variation, color distortions, shape distortions, cropping, shifting, and rotation. Compared with several existing systems, our system in general achieves more accurate retrieval at higher speed.
(This work was supported in part by the National Science Foundation's Digital Libraries initiative. The authors would like to thank the help of Oscar Firschein and anonymous reviewers.)
With the steady growth of computer power, rapidly declining cost of storage, and ever-increasing access to the Internet, digital acquisition of information has become increasingly popular in recent years. Digital information is preferable to analog formats because of convenient sharing and distribution properties. This trend has motivated research in image databases, which were nearly ignored by traditional computer systems due to the enormous amount of data necessary to represent images and the difficulty of automatically analyzing images. Currently, storage is less of an issue since huge storage capacity is available at low cost. However, effective indexing and searching of large-scale image databases remains as a challenge for computer systems. The automatic derivation of semantics from the content of an image is the focus of interest for most research on image databases. Image semantics has several levels: semantic types, object composition, abstract semantics, and detailed semantics.
Content-based image retrieval is defined as the retrieval of relevant images from an image database based on automatically derived imagery features. The need for efficient content-based image retrieval has increased tremendously in many application areas such as biomedicine, crime prevention, military, commerce, culture, education, entertainment, and Web image classification and searching.
There are many general-purpose image search engines. In the commercial domain, IBM QBIC [3,16] is one of the earliest developed systems. Recently, additional systems have been developed at IBM T.J. Watson [23], VIRAGE [5], NEC AMORA [14], Bell Laboratory [15], Interpix (Yahoo), Excalibur, and Scour.net. In the academic domain, MIT Photobook [17,18] is one of the earliest. Berkeley Blobworld [1], Columbia VisualSEEK and WebSEEK [22], CMU Informedia [24], UIUC MARS [12], UCSB NeTra [10], UCSD, Stanford (EMD [19], WBIIS [26]) are some of the recent systems.
Existing general-purpose CBIR systems roughly fall into three categories depending on the signature extraction approach used: histogram, color layout, and region-based search. There are also systems that combine retrieval results from individual algorithms by a weighted sum matching metric [5], or other merging schemes [20].
Histogram search [16,19] characterizes an image by its color distribution, or histogram. The drawback of a global histogram representation is that information about object location, shape, and texture is discarded. Color histogram search is sensitive to intensity variation, color distortions, and cropping.
The color layout approach attempts to mitigate the problems with histogram search. For traditional color layout indexing [16], images are partitioned into blocks and the average color of each block is stored. Thus, the color layout is essentially a low resolution representation of the original image. A later system, WBIIS [26], uses significant Daubechies' wavelet coefficients instead of averaging. By adjusting block sizes or the levels of wavelet transforms, the coarseness of a color layout representation can be tuned. The finest color layout using a single pixel block is merely the original image. We can hence view a color layout representation as an opposite extreme of a histogram. At proper resolutions, the color layout representation naturally retains shape, location, and texture information. However, as with pixel representation, although information such as shape is preserved in the color layout representation, the retrieval system cannot ``see'' it explicitly. Color layout search is sensitive to shifting, cropping, scaling, and rotation because images are characterized by a set of local properties.
Region-based retrieval systems attempt to overcome the deficiencies of color layout search by representing images at the object-level. A region-based retrieval system applies image segmentation to decompose an image into regions, which correspond to objects if the decomposition is ideal. The object-level representation is intended to be close to the perception of the human visual system (HVS).
Since the retrieval system has identified objects in the image, it is relatively easy for the system to recognize similar objects at different locations and with different orientations and sizes. Region-based retrieval systems include the Netra system [10], the Blobworld system [1], and the query system with color region templates [23]. We have developed SIMPLIcity (Semantics-sensitive Integrated Matching for Picture LIbraries), a region-based image retrieval system, using high-level semantics classification [27].
The NeTra and the Blobworld systems compare images based on individual regions. Although querying based on a limited number of regions is allowed, the query is performed by merging single-region query results. Because of the great difficulty of achieving accurate segmentation, systems in [10,1] tend to partition one object into several regions with none of them being representative for the object, especially for images without distinctive objects and scenes. Consequently, it is often difficult for users to determine which regions and features should be used for retrieval.
Not much attention has been paid to developing similarity measures that combine information from all of the regions. One effort in this direction is the querying system developed by Smith and Li [23]. Their system decomposes an image into regions with characterizations pre-defined in a finite pattern library. With every pattern labeled by a symbol, images are then represented by region strings. Region strings are converted to composite region template (CRT) descriptor matrices reflecting the relative ordering of symbols. Similarity between images is measured by the closeness between the CRT descriptor matrices. This measure is sensitive to object shifting since a CRT matrix is determined solely by the ordering of symbols. Robustness to scaling and rotation is not considered by the measure either. Because the definition of the CRT descriptor matrix relies on the pattern library, the system performance depends critically on the library. Performance degrades if regions in an image are not represented in the library. The system in [23] uses a CRT library with patterns described only by color. In particular, the patterns are obtained by quantizing color space. If texture and shape features are added to distinguish patterns, the number of patterns in the library will increase dramatically, roughly exponentially in the number of features if patterns are obtained by uniformly quantizing features.
To reflect semantics more precisely by the region representation, we have developed IRM, a similarity measure of images based on region representations. IRM incorporates the properties of all the segmented regions so that information about an image can be fully used. Region-based matching is a difficult problem because of inaccurate segmentation. Semantically-precise image segmentation is extremely difficult [21,11,28,7,8] and is still an open problem in computer vision. For example, segmentation algorithm may segment an image of a dog into two regions: the dog and the background. The same algorithm may segment another image of a dog into six regions: the body of the dog, the front leg(s) of the dog, the rear leg(s) of the dog, the eye(s), the background grass, and the sky.

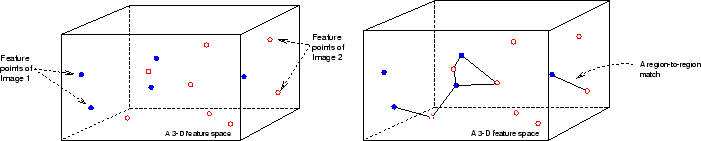
Figure 1: Region-to-region matching results are incorporated in the Integrated Region Matching (IRM) metric. A 3-D feature space is shown to illustrate the concept.
The IRM measure we have developed has the following major advantages:
To define the similarity measure, we first attempt to match regions in two images. Being aware that segmentation cannot be perfect, we ``soften'' the matching by allowing one region of an image to be matched to several regions of another image. Here, a region-to-region match is obtained when the regions are relatively similar to each other in terms of the features extracted.
The principle of matching is that the closest region pair is matched first. We call this matching scheme Integrated Region Matching (IRM) to stress the incorporation of regions in the retrieval process. After regions are matched, the similarity measure is computed as a weighted sum of the similarity between region pairs, with weights determined by the matching scheme. Figure 1 illustrates the concept of IRM in a 3-D feature space. The features we extract on the segmented regions are of high dimensions. The problem is much more sophisticated in a high-dimensional feature space.
The remainder of the paper is organized as follows. In Section 2, the similarity measure based on segmented regions is defined. In Section 3, we describe the experiments we have performed and provide results. We conclude in Section 4.
The similarity measure is defined based on segmented regions of images. Our system segments images based on color and frequency features using the k-means algorithm [6]. For general-purpose images such as the images in a photo library or the images on the World-Wide Web (WWW), precise object segmentation is nearly as difficult as computer semantics understanding. Semantically-precise segmentation, however, is not crucial to our system because we use a more robust integrated region-matching (IRM) scheme which is insensitive to inaccurate segmentation (Figure 2).
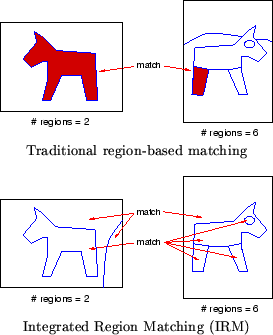
Figure 2: Integrated Region Matching (IRM) is robust to poor image segmentation.
To segment an image, the system partitions the image into blocks with 4 x 4 pixels and extracts a feature vector for each block. We choose this block size to optimize between texture effectiveness and segmentation coarseness. The k-means algorithm is used to cluster the feature vectors into several classes with every class corresponding to one region in the segmented image. An alternative to the block-wise segmentation is a pixel-wise segmentation by forming a window centered around every pixel.
The segmentation results are available on the demonstration web site. One main advantage of using the k-means clustering algorithm for segmentation is that blocks in each cluster does not have to be neighboring blocks. This way, we preserve the natural clustering of objects and allow classification of textured images [9]. The number of regions, k, is selected adaptively. Experimental results have shown that the system is insensitive to the number of regions segmented.
Six features are used for segmentation. Three of them are the average color components in a 4 x 4 block. The other three represent energy in high frequency bands of the wavelet transforms [2,13], that is, the square root of the second order moment of wavelet coefficients in high frequency bands. We use the well-known LUV color space, where L encodes luminance, and U and V encode color information (chrominance).
To obtain the other three features, a Daubechies-4 wavelet transform is
applied to the L component of the image. After a one-level wavelet
transform, a 4 x 4 block is decomposed into four frequency
bands: the LL, LH, HL, and HH bands [2]. Each
band contains 2 x 2 coefficients. Without loss of generality,
suppose the coefficients in the HL band are
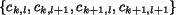 . One feature is:
. One feature is:
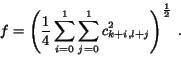
The other two features are computed similarly from the LH and HH bands. The motivation for using the features extracted from high frequency bands is that they reflect texture properties. Moments of wavelet coefficients in various frequency bands have been shown to be effective for representing texture [25]. The intuition behind this is that coefficients in different frequency bands show variations in different directions. For example, the HL band shows activities in the horizontal direction. An image with vertical strips thus has high energy in the HL band and low energy in the LH band.
In this section, we define the similarity measure between two sets of
regions. Assume that Image 1 and 2 are represented by region sets
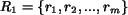 and
and
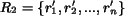 , where
, where
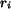 or
or 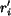 is the descriptor of region
is the descriptor of region
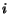 . Denote the
distance between region
. Denote the
distance between region 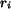 and
and 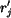 as
as 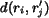 , which is
written as
, which is
written as 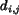 in short. Details about features included in
in short. Details about features included in
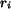 and the definition of
and the definition of 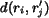 will be discussed later.
To compute the similarity measure between region sets
will be discussed later.
To compute the similarity measure between region sets 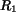 and
and 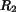 ,
,
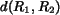 , we first match all regions in the two images. When we
judge the similarity of two animal photographs, we usually compare the
animals in the images before comparing the background areas in the
images. The overall similarity of the two images depends on the
closeness in the two aspects. The correspondence between objects in
the images is crucial to our judgment of similarity since it would be
meaningless to compare the animal in one image with the background in
another. Our IRM matching scheme aims at building correspondence
between regions that is consistent with human perception. To increase
robustness against segmentation errors, we allow a region to be
matched to several regions in another image. A matching between
, we first match all regions in the two images. When we
judge the similarity of two animal photographs, we usually compare the
animals in the images before comparing the background areas in the
images. The overall similarity of the two images depends on the
closeness in the two aspects. The correspondence between objects in
the images is crucial to our judgment of similarity since it would be
meaningless to compare the animal in one image with the background in
another. Our IRM matching scheme aims at building correspondence
between regions that is consistent with human perception. To increase
robustness against segmentation errors, we allow a region to be
matched to several regions in another image. A matching between 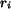 and
and 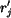 is assigned with a significance credit
is assigned with a significance credit 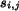 ,
,
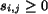 . The significance credit indicates the importance of
the matching for determining similarity between images. The matrix
. The significance credit indicates the importance of
the matching for determining similarity between images. The matrix
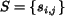 ,
,
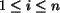 ,
,
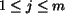 , is referred to as
the significance matrix.
, is referred to as
the significance matrix.
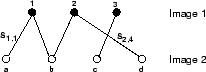
Figure 3: Integrated region matching (IRM) allows one region to be matched to several regions.
A graphical explanation of the integrated matching scheme is provided in Figure 3. The figure shows that matching between images can be represented by an edge weighted graph in which every vertex in the graph corresponds to a region. If two vertices are connected, the two regions are matched with a significance credit being the weight on the edge. To distinguish from matching two sets of regions, we refer to the matching of two regions as they are linked. The length of an edge can be regarded as the distance between the two regions represented. If two vertices are not connected, the corresponding regions are either from the same image or the significance credit of matching them is zero. Every matching between images is characterized by links between regions and their significance credits. The matching used to compute the distance between two images is referred to as the admissible matching. The admissible matching is specified by conditions on the significance matrix. If a graph represents an admissible matching, the distance between the two region sets is the summation of all the weighted edge lengths, i.e.,
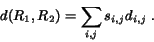
We call this distance the integrated region matching (IRM) distance.
The problem of defining distance between region sets is then converted
to choosing the significance matrix 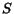 . A natural issue to raise is
what constraints should be put on
. A natural issue to raise is
what constraints should be put on 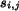 so that the admissible
matching yields good similarity measure. In other words, what
properties do we expect an admissible matching to possess? The first
property we want to enforce is the fulfillment of significance.
Assume that the significance of
so that the admissible
matching yields good similarity measure. In other words, what
properties do we expect an admissible matching to possess? The first
property we want to enforce is the fulfillment of significance.
Assume that the significance of 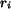 in Image 1 is
in Image 1 is 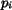 , and
, and 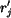 in Image 2 is
in Image 2 is 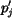 , we require that
, we require that
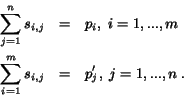
For normalization, we have
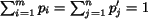 .
The fulfillment of significance ensures that all the regions play a
role for measuring similarity. We also require an admissible matching
to link the most similar regions at the highest priority. For
example, if two images are the same, the admissible matching should
link a region in Image 1 only to the same region in Image 2. With
this matching, the distance between the two images equals zero, which
coincides with our intuition. Following the ``most similar highest
priority (MSHP)'' principle, the IRM algorithm attempts to fulfill the
significance credits of regions by assigning as much significance as
possible to the region link with minimum distance. Initially, assume
that
.
The fulfillment of significance ensures that all the regions play a
role for measuring similarity. We also require an admissible matching
to link the most similar regions at the highest priority. For
example, if two images are the same, the admissible matching should
link a region in Image 1 only to the same region in Image 2. With
this matching, the distance between the two images equals zero, which
coincides with our intuition. Following the ``most similar highest
priority (MSHP)'' principle, the IRM algorithm attempts to fulfill the
significance credits of regions by assigning as much significance as
possible to the region link with minimum distance. Initially, assume
that 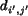 is the minimum distance, we set
is the minimum distance, we set
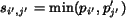 . Without loss of generality, assume
. Without loss of generality, assume
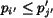 . Then
. Then 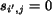 , for
, for 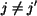 since the
link between region
since the
link between region 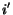 and
and 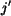 has filled the significance of
region
has filled the significance of
region 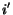 . The significance credit left for region
. The significance credit left for region 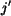 is reduced
to
is reduced
to
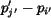 . The updated matching problem is then solving
. The updated matching problem is then solving
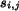 ,
, 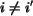 , by the MSHP rule under constraints:
, by the MSHP rule under constraints:
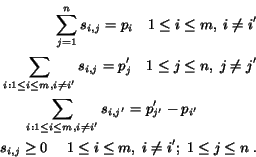
We apply the previous procedure to the updated problem. The
iteration stops when all the significance credits 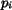 and
and 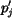 have
been assigned. The algorithm is summarized as follows.
have
been assigned. The algorithm is summarized as follows.
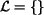 , denote
, denote
 .
.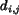 for
for
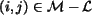 .
Label the corresponding
.
Label the corresponding 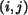 as
as 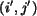 .
. 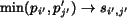 .
.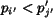 , set
, set 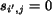 ,
, 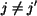 ; otherwise,
set
; otherwise,
set 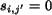 ,
, 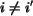 .
. 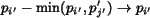 .
. 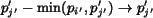 .
. 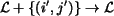 .
.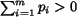 and
and
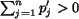 , go to Step
2; otherwise, stop.
, go to Step
2; otherwise, stop.
We now come to the issue of choosing 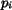 . The value of
. The value of 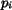 is
chosen to reflect the significance of region
is
chosen to reflect the significance of region 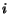 in the image. If we
assume that every region is equally important, then
in the image. If we
assume that every region is equally important, then 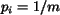 , where
, where
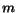 is the number of regions. In the case that Image 1 and Image 2
have the same number of regions, a region in Image
is the number of regions. In the case that Image 1 and Image 2
have the same number of regions, a region in Image 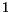 is matched
exclusively to one region in Image 2. Another choice of
is matched
exclusively to one region in Image 2. Another choice of 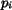 is the
percentage of the image covered by region i based on the view that
important objects in an image tend to occupy larger areas. We refer
to this assignment of
is the
percentage of the image covered by region i based on the view that
important objects in an image tend to occupy larger areas. We refer
to this assignment of 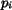 as the area percentage scheme. This
scheme is less sensitive to inaccurate segmentation than the uniform
scheme. If one object is partitioned into several regions, the
uniform scheme raises its significance improperly, whereas the area
percentage scheme retains its significance. On the other hand, if
objects are merged into one region, the area percentage scheme assigns
relatively high significance to the region. The current
implementation of the system uses the area percentage scheme.
as the area percentage scheme. This
scheme is less sensitive to inaccurate segmentation than the uniform
scheme. If one object is partitioned into several regions, the
uniform scheme raises its significance improperly, whereas the area
percentage scheme retains its significance. On the other hand, if
objects are merged into one region, the area percentage scheme assigns
relatively high significance to the region. The current
implementation of the system uses the area percentage scheme.
The scheme of assigning significance credits can also take region
location into consideration. For example, higher significance may be
assigned to regions in the center of an image than to those around
boundaries. Another way to count location in the similarity measure
is to generalize the definition of the IRM distance to
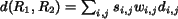 .
The parameter
.
The parameter 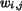 is chosen to adjust the effect of region i
and j on the similarity measure. In the current system, regions
around boundaries are slightly down-weighted by using this generalized
IRM distance.
is chosen to adjust the effect of region i
and j on the similarity measure. In the current system, regions
around boundaries are slightly down-weighted by using this generalized
IRM distance.
The distance between a region pair, 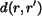 , is determined by the
color, texture, and shape characteristics of the regions. We have
described in Section 2.1 the features used by the
, is determined by the
color, texture, and shape characteristics of the regions. We have
described in Section 2.1 the features used by the 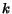 -means
algorithm for segmentation. The mean values of these features in one
cluster are used to represent color and texture in the corresponding
region. To describe shape, normalized inertia [4] of
order
-means
algorithm for segmentation. The mean values of these features in one
cluster are used to represent color and texture in the corresponding
region. To describe shape, normalized inertia [4] of
order 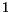 to
to 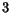 are used. For a region
are used. For a region  in
in 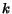 dimensional
Euclidean space
dimensional
Euclidean space
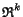 , its normalized inertia of order
, its normalized inertia of order
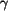 is
is
![\begin{eqnarray*}
l(H, \gamma)=\frac{\int_{H}\Vert x-{\hat x}\Vert^{\gamma}dx}{[V(H)]^{1+\gamma/k}}
\end{eqnarray*}](img69.gif)
where 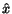 is the centroid of
is the centroid of 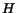 and
and 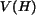 is the volume of
is the volume of 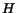 .
Since an image is specified by pixels on a grid, the discrete form of
the normalized inertia is used, that is,
.
Since an image is specified by pixels on a grid, the discrete form of
the normalized inertia is used, that is,
![\begin{eqnarray*}
l(H, \gamma)=
\frac{\sum_{x: x\in H}\Vert x-{\hat x}\Vert^{\gamma}}{[V(H)]^{1+\gamma/k}}
\end{eqnarray*}](img72.gif)
where 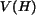 is the number of pixels in region
is the number of pixels in region 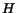 .
The normalized inertia is invariant with scaling and rotation. The minimum
normalized inertia is achieved by spheres. Denote the
.
The normalized inertia is invariant with scaling and rotation. The minimum
normalized inertia is achieved by spheres. Denote the 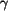 th order
normalized inertia of spheres as
th order
normalized inertia of spheres as 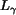 .
We define shape features as
.
We define shape features as 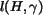 normalized by
normalized by 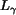 :
:
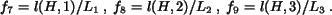
The computation of shape features is skipped for textured images
because region shape is not perceptually important for such images.
By a textured image, we refer to an image composed of repeated
patterns that appears like a unique texture surface. Automatic
classification of textured and non-textured images is implemented in
our system (for details see [9]). For textured image,
the region distance 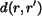 is defined as
is defined as
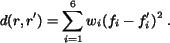
For non-textured images, 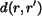 is defined as
is defined as
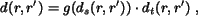
where 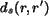 is the shape distance computed by
is the shape distance computed by
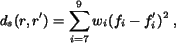
and 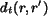 is the color and texture distance defined the same as
the distance between textured image regions, i.e.,
is the color and texture distance defined the same as
the distance between textured image regions, i.e.,
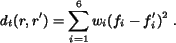
The function 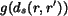 is a converting function to ensure a
proper influence of the shape distance on the total distance. In our
system, it is defined as
is a converting function to ensure a
proper influence of the shape distance on the total distance. In our
system, it is defined as
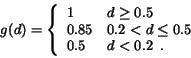
It is observed that when
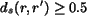 , the two regions bear
little resemblance. It is then not meaningful to distinguish the
extent of similarity by
, the two regions bear
little resemblance. It is then not meaningful to distinguish the
extent of similarity by 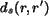 because perceptually the two
regions simply appear different. We thus set
because perceptually the two
regions simply appear different. We thus set 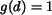 for
for 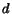 greater
than a threshold. When
greater
than a threshold. When 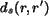 is very small, to retain the
influence of color and texture,
is very small, to retain the
influence of color and texture, 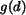 is bounded away from zero. For
simplicity,
is bounded away from zero. For
simplicity, 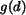 is selected as a piece-wise constant function
instead of a smooth one. Because rather simple shape features are
used in our system, color and texture are emphasized more than shape
for determining similarity between regions. As can be seen from the
definition of
is selected as a piece-wise constant function
instead of a smooth one. Because rather simple shape features are
used in our system, color and texture are emphasized more than shape
for determining similarity between regions. As can be seen from the
definition of 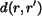 , the shape distance serves as a ``bonus'' in
the sense that only when two regions are considerably similar in
shape, their distance is affected by shape.
, the shape distance serves as a ``bonus'' in
the sense that only when two regions are considerably similar in
shape, their distance is affected by shape.
There has been much work on developing distance between regions. Since the integrated region matching scheme is not confined to any particular region distance and defining a region distance is not our main interest, we have chosen a distance with low computational cost so that the system can be tested on a large image database.
The IRM has been implemented as a part of our experimental SIMPLIcity image retrieval system. We tested the system on a general-purpose image database (from COREL) including about 200,000 pictures, which are stored in JPEG format with size 384 x 256 or 256 x 384. These images were automatically classified into three semantic types: graph (clip art), textured photograph, and non-textured photograph [9]. For each image, the features, locations, and areas of all its regions are stored.
Compared with two color histogram systems [19] and the WBIIS (Wavelet-Based Image Indexing and Searching) system [26], our system in general achieves more accurate retrieval at higher speed. However, it is difficult to design a fair comparison with existing region-based searching algorithms such as the Blobworld system which depends on manually defined complicated queries. An on-line demonstration is provided. Readers are encouraged to visit the web site since we cannot show many examples here due to limited space.
The SIMPLIcity system was compared with the WBIIS system using the same image database. As WBIIS forms image signatures using wavelet coefficients in the lower frequency bands, it performs well with relatively smooth images, such as most landscape images. For images with details crucial to semantics, such as pictures containing people, the performance of WBIIS degrades. In general, the SIMPLIcity system performs as well as WBIIS for smooth landscape images. Examples are omitted due to limited space.

Figure 4: Comparison of SIMPLIcity and WBIIS. The query image (upper-left corner) is a photo of food. Best 11 matches are shown.
SIMPLIcity also performs well for images composed of fine details. Retrieval results with a photo of a hamburger as the query are shown in Figure 4. The query image is the image at the upper-left corner. The three numbers below the pictures from left to right are: the ID of the image in the database, the value of the similarity measure between the query image and the matched image, and the number of regions in the image. The SIMPLIcity system retrieves 10 images with food out of the first 11 matched images. The WBIIS system, however, does not retrieve any image with food in the first 11 matches. The top match made by SIMPLIcity is also a photo of hamburger, which is perceptually very close to the query image. WBIIS misses this image because the query image contains important fine details, which are smoothed out by the multi-level wavelet transform in the system.

Figure 5: Retrieval by SIMPLIcity: the query image is a portrait image that probably depicts life in Africa.
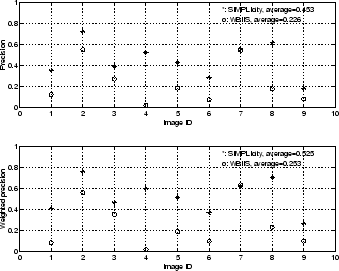
Figure 6: Comparison of SIMPLIcity and WBIIS: average precisions and weighted precisions of 9 image categories.
| 1. Sports and public events | 2. Beach | 3. Food |
| 4. Landscape with buildings | 5. Portrait | 6. Horses |
| 7. Tools and toys | 8. Flowers | 9. Vehicle |
Table 1: Categories of images tested in our systematic evaluation.
Another query example is shown in Figure 5. The query image in Figure 5 is difficult to match because objects in the image are not distinctive from the background. Moreover, the color contrast is small. Among the retrieved images, only the third matched image is not a picture of a person. A few images, the 1st, 4th, 7th, and 8th matches, depict a similar topic as well, probably about life in Africa.
To provide numerical results, we tested 27 sample images chosen randomly from 9 categories, each containing 3 of the images. Image matching is performed on the COREL database of 200,000 images. A retrieved image is considered a match if it belongs to the same category of the query image. The categories of images tested are listed in Table 1. Most categories simply include images containing the specified objects. Images in the ``sports and public events'' class contain humans in a game or public event, such as festival. Portraits are not included in this category. The ``landscape with buildings'' class refers to outdoor scenes featuring man-made constructions such as buildings and sculptures. The ``beach'' class refers to sceneries at coasts or river banks. For the ``portrait'' class, an image has to show people as the main feature. A scene with human beings as a minor part is not included.
Precision was computed for both SIMPLIcity and WBIIS. Recall was not
calculated because the database is large and it is difficult to
estimate the total number of images in one category, even
approximately. To account for the ranks of matched images, the
average of precisions within 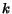 retrieved images,
retrieved images, 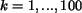 , is
computed, that is,
, is
computed, that is,
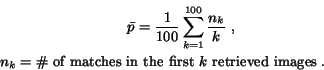
This average precision is referred to as the ``weighted precision''
because it is equivalent to a weighted percentage of matched images
with a larger weight assigned to an image retrieved at a higher rank.
For each of the 9
image categories, the average precision and
weighted precision based on the 3
sample images are plotted in
Figure 6. The image category identification number is
assigned according to Table 1 scanned row wise.
Except for the tools and toys category, in which case the two systems
perform about equally well, SIMPLIcity has achieved better results
than WBIIS measured in both ways. For the two categories of landscape
with buildings and vehicle, the difference between the two system is
quite significant. On average, the precision and the weighted
precision of SIMPLIcity are higher than those of WBIIS by 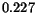 and
and
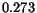 respectively.
respectively.
The SIMPLIcity system was also evaluated based on a subset of the COREL database, formed by 10 image categories, each containing 100 pictures. Within this database, it is known whether any two images are of the same category. In particular, a retrieved image is considered a match if and only if it is in the same category as the query. This assumption is reasonable since the 10 categories were chosen so that each depicts a distinct semantic topic. Every image in the sub-database was tested as a query, and the retrieval ranks of all the rest images were recorded. Three statistics were computed for each query: the precision within the first 100 retrieved images, the mean rank of all the matched images, and the standard deviation of the ranks of matched images.
The recall within the first 100 retrieved images was not computed
because it is proportional to the precision in this special case. The
total number of semantically related images for each query is fixed to
be 100. The average performance for each image category in terms of
the three statistics is listed in Table 2, where
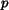 denotes precision,
denotes precision, 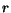 denotes the mean rank of matched images,
and
denotes the mean rank of matched images,
and 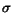 denotes the standard deviation of the ranks of matched
images. For a system that ranks images randomly, the average
denotes the standard deviation of the ranks of matched
images. For a system that ranks images randomly, the average 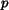 is
about
is
about 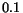 , and the average
, and the average 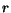 is about
is about 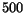 .
.
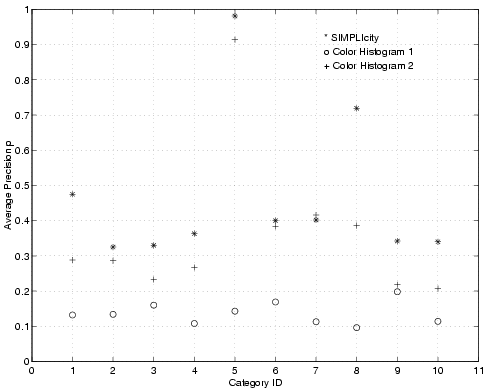
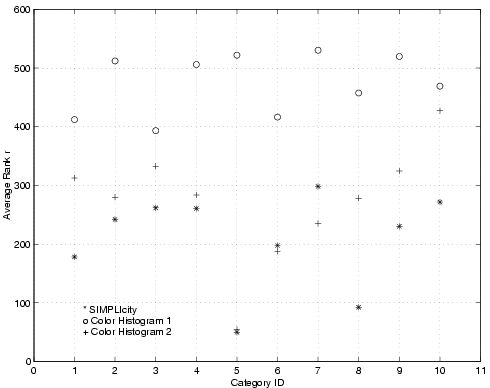
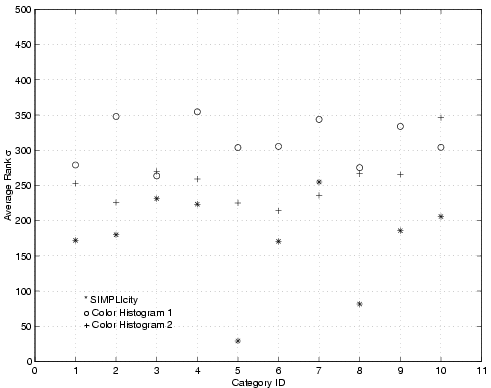
Figure 7:
Comparing with color histogram methods on average precision 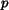 ,
average rank of matched images
,
average rank of matched images 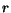 , and the standard deviation of the
ranks of matched images
, and the standard deviation of the
ranks of matched images 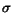 . The lower numbers indicate
better results for the last two plots (i.e., the
. The lower numbers indicate
better results for the last two plots (i.e., the 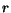 plot and the
plot and the
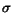 plot). Color Histogram 1 gives an average of 13.1 filled
color bins per image, while Color Histogram 2 gives an average of 42.6
filled color bins per image. SIMPLIcity partitions an image into an
average of only 4.3 regions.
plot). Color Histogram 1 gives an average of 13.1 filled
color bins per image, while Color Histogram 2 gives an average of 42.6
filled color bins per image. SIMPLIcity partitions an image into an
average of only 4.3 regions.
| Category | Average 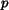 |
Average 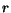 |
Average 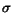 |
| 1. Africa | 0.475 | 178.2 | 171.9 |
| 2. Beach | 0.325 | 242.1 | 180.0 |
| 3. Buildings | 0.330 | 261.8 | 231.4 |
| 4. Buses | 0.363 | 260.7 | 223.4 |
| 5. Dinosaurs | 0.981 | 49.7 | 29.2 |
| 6. Elephants | 0.400 | 197.7 | 170.7 |
| 7. Flowers | 0.402 | 298.4 | 254.9 |
| 8. Horses | 0.719 | 92.5 | 81.5 |
| 9. Mountains | 0.342 | 230.4 | 185.8 |
| 10. Food | 0.340 | 271.7 | 205.8 |
Table 2:
The average performance
for each image category evaluated by precision 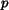 , the mean
rank of matched images
, the mean
rank of matched images 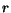 , and the standard deviation of the ranks
of matched images
, and the standard deviation of the ranks
of matched images 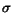 .
.
Similar evaluation tests were carried out for color histogram match. We used LUV color space and a matching metric similar to the EMD described in [19] to extract color histogram features and match in the categorized image database. Two different color bin sizes, with an average of 13.1 and 42.6 filled color bins per image, were evaluated. We call the one with less filled color bins the Color Histogram 1 system and the other the Color Histogram 2 system. Figure 7 shows the performance as compared with the SIMPLIcity system. Clearly, both of the two color histogram-based matching systems perform much worse than the SIMPLIcity region-based CBIR system in almost all image categories. The performance of the Color Histogram 2 system is better than that of the Color Histogram 1 system due to more detailed color separation obtained with more filled bins. However, the Color Histogram 2 system is so slow that it is impossible to obtain matches on larger databases. SIMPLIcity runs at about twice the speed of the faster Color Histogram 1 system and gives much better searching accuracy than the slower Color Histogram 2 system.
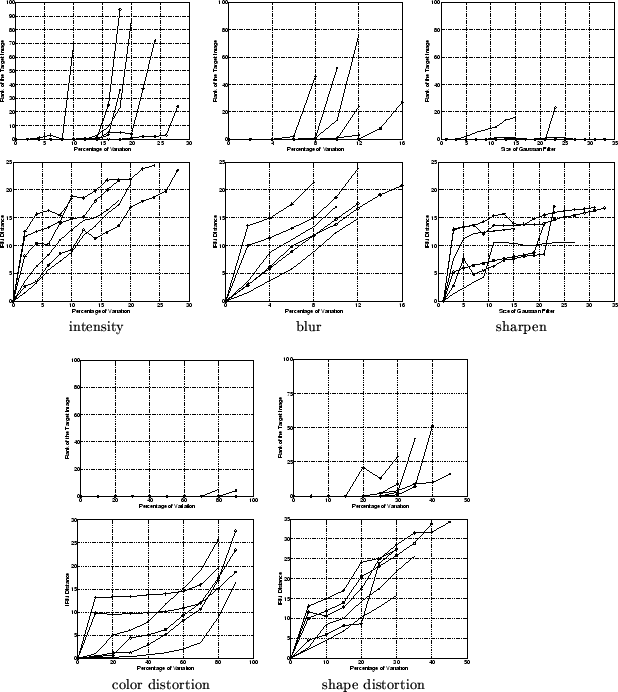
Figure 8: The robustness of the system to image alterations.
We have performed extensive experiments to test the robustness of the system. Figure 8 summarizes the results. The graphs in the first row show the the changes in ranking of the target image as we increase the significance of image alterations. The graphs in the second row show the the changes in IRM distance between the altered image and the target image, as we increase the significance of image alterations.

Figure 9: The robustness of the system to image alterations. Best 5 matches are shown.
The system is exceptionally robust to image alterations such as intensity variation, sharpness variation, intentional color distortions, intentional shape distortions, cropping, shifting, and rotation. Figure 9 shows some query examples, using the 200,000-image COREL database.
The algorithm has been implemented on a Pentium Pro 430MHz PC using the Linux operating system. To compute the feature vectors for the 200,000 color images of size 384 x 256 in our general-purpose image database requires approximately 60 hours. On average, one second is needed to segment an image and to compute the features of all regions. The speed is much faster than other region-based methods. For example, the Blobworld system developed by University of California at Berkeley segments each image in several minutes. Fast indexing has provided us with the capability of handling outside queries and sketch queries in real-time.
The matching speed is very fast. When the query image is in the database, it takes about 1.5 seconds of CPU time on average to sort all the images in the 200,000-image database using our similarity measure. If the query is not in the database, one extra second of CPU time is spent to process the query. Other systems we have tested are several times slower.
A measure for the overall similarity between images, defined by a region-matching scheme that incorporates properties of all the regions in the images. Compared with retrieval based on individual regions, the overall similarity approach in IRM reduces the influence of inaccurate segmentation, helps to clarify the semantics of a particular region, and enables a simple querying interface for region-based image retrieval systems. The application of the system to a database of about 200,000 general-purpose images shows more accurate and faster retrieval compared with existing algorithms. Additionally, the system is robust to various image alterations.
The IRM can be improved by introducing weights on different regions, refining the features, and allowing the user to turn off the scale-invariance and rotation-invariance characteristics. The interface can be improved by providing more intuitive similarity distances. We are also planning to extend the IRM to special image databases (e.g., biomedical), and very large image databases (e.g., WWW).
Other versions: Postscript, PDF.