|
CS245 PROBLEM SET #2
Due by Wednesday, July 19, 2000
|
Please keep your answers concise and clear. We may take off points for
extremely lengthy and messy answers.
Problem 1: Conventional Indexes (20 points)
Consider two relations R(A, B) and S(B, C)
stored as sequential files. There are two types of most frequently
asked queries as follows.
- Q1:
- select * from R where R.A > a1 and R.A < a2
- Q2:
- select * from R, S where R.B = S.B
Suppose that we are allowed to build conventional dense, sparse, or multi-level
indexes over the relations to optimize the above queries. What indexes shall
we build over R and S to obtain the best query performance?
Briefly specify the following aspects for each index you choose to build.
- a)
- What is the type of the index (dense, sparse, or multi-level)?
- b)
- Which attribute is the index built on?
- c)
- Is it a primary or a secondary index?
- d)
- How should we use the index for the queries?
Problem 2: B+-tree and B-tree (20 points)
Consider a DBMS that has the following characteristics:
- 2KB fixed-size blocks
- 12-byte pointers
- 56-byte block headers
We want to build an index on a search key that is 8 bytes long.
Calculate the maximum number of records we can index with
- a)
- a 3-level B+ tree (2 levels plus the root)
- b)
- a 3-level B tree
Problem 3: B+-tree Insertions and Deletions (20 points)
Consider the above B+ tree.
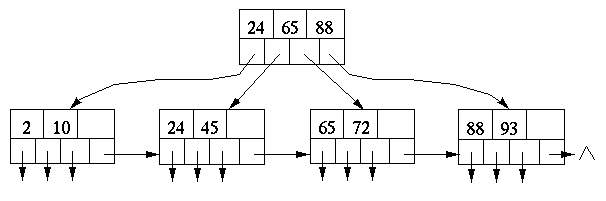
Show the B+ tree that results after inserting (in the given order) 56, 50, 75,
87, 48. From that resulting B+ tree we delete (in the given order) 50, 24, 65,
93, 75. What is the resulting final B+ tree?
Problem 4: Extensible and Linear Hashing (20 points)
Consider a dynamic hash structure where buckets can hold up to three records.
Initially the structure is empty. Then we insert the following records, in the
order below, where we indicate the hashed key in parenthesis (in binary):
a [010000]
b [011010]
c [111100]
d [001110]
e [010111]
f [011010]
g [101001]
h [010111]
i [000110]
j [101001]
- a)
- Show the extensible hash structure after these records have been inserted.
- b)
- Show the linear hash structure after these records have been inserted.
Assume that the threshold value is 2. (i.e., when the average number of keys
per non-overflow bucket is greater than 2, we allocate another bucket).
Problem 5: Multiple-Key Index (20 points)
There is a relation R(X, Y, Z) where the pair of attributes
X and Y together form the key. Suppose that for each
X there are records with 1024 different values of Y,
and for each Y there are records with 1024 different values of
X. We need to answer queries of the form "select Z from R where
C", where C is the selection condition. Suppose we know that
- 1)
- C is "X = x" in 20% of the cases
- 2)
- C is "Y = y" in 30% of the cases
- 3)
- C is "X = x and Y = y" in 50% of the cases
for various constants x and y.
We want to build an index for the relation to improve the average query
performance, and we have the following options:
- a)
- Build a multiple-key index with X as the first attribute
- b)
- Build a multiple-key index with Y as the first attribute
- c)
- Build two secondary indexes on X and Y, using the
"pointer bucket" technique (described in the lecture) to deal with duplicate
values.
Both the index and the relation are stored on disk. Suppose that each
X or Y value is 8 bytes long, a record pointer is 8 bytes
long, and a block is 8K bytes. Compute the average query cost (number of block
I/Os) for each index option, and pick the best index.