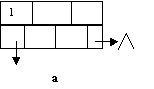
CS245 Summer 2000 Solution Set for Homework 3

Problem 1

(a) Since the blocks are stored sequentially, we only need a pointer to the first block. The first block of the index will have a block pointer to the first file block and key values. The rest of the index block will only have key values.
We can fit
ë(2048-8) / 12) û = 170 keys in the first index block and
ë2048/12 û = 170 keys in the remaining blocks.
The total number of blocks we need is
1+ é(500000-170)/170 ù=2942 blocks.

(b) Since the blocks are not contiguous, we need a block pointer for every block. Each entry will be
8 bytes(pointer) + 12 bytes(key) = 20 bytes.
We can fit
ë(2048 / 20) û = 102 key pointer pairs in a block.
The total number of blocks we need is
é500000 / 102 ù=4902 blocks.

(c) Since blocks are not contiguous, we need a pointer for each block. We can fit
ë(2048 / 20) û = 102 key pointer pairs in a block.
The total number of blocks we need is
é4902/ 102 ù=49 blocks.

(d) This question can be answered in two ways depending on whether you want a block pointer or a record pointer for each key. If duplicate keys exists, it is better to use record pointers instead of block pointers for simplicity in implementation.

Solution with block pointers:
Size of entry = 12 (key) + 8 (pointer) = 20 bytes
ë2048 / 20) û = 102 key pointer pairs in a block. Number of blocks needed:
é10000000/ 102 ù=98040 blocks.

Solution with record pointers:
Size of entry = 12 (key) + 9 (pointer) = 21 bytes
ë2048 / 21) û = 97 key pointer pairs in a block. Number of blocks needed:
é10000000/ 97 ù=103093 blocks.

(e) Since the index blocks are contiguous, we only need a pointer to the first block and the key values. We can fit
ë(2048-8) / 12) û = 170 keys in the first index block and
ë2048 / 12 û = 170

Solution with block pointers:
The total number of block we need is
1+ é(98040-170)/ 170 ù=577 blocks.

Solution with record pointers:
The total number of block we need is
1+ é(103093-170)/ 170 ù=607 blocks.

Problem 2

Note 1: Diagrams by courtesy of Frank Luo.

Note 2: Alternate solutions are possible depending on how the keys are redistributed after splitting a node. All valid solutions were given full credit.

Problem 3

(a) Root should have at least 2 children. Each child are now leaf and has at least ë(n+1) / 2û record pointers.

Minimum number of record pointers = 2 * ë(n+1) / 2û

(b) Again, root has 2 children. Each non-leaf node has at least é(n+1) / 2ù pointers. So there are 2 * é(n+1) / 2ù leaf nodes. Each leaf node has ë(n+1) / 2û record pointers.

Minimum number of record pointers = 2 * é(n+1) / 2ù * ë(n+1) / 2û

Minimum number of record pointers = 2 * ( é(n+1) / 2ù ) ^j- 2 * ë(n+1) / 2û

(d) From (c), a B+ tree with j levels has at least 2 * ( é(n+1) / 2ù ) ^j- 2 * ë(n+1) / 2û records.

r ł 2 * ( é(n+1) / 2ù ) ^j- 2 * ë(n+1) / 2û

j – 2 Ł ( log r – log 2 – log ( ë(n+1) / 2û ) ) / log ( é(n+1) / 2ù )

j Ł 2 + ( log r – log 2 – log ( ë(n+1) / 2û ) ) / log ( é(n+1) / 2ù )

Common errors:

* Think the root is like normal non-leaf nodes and has é(n+1) / 2ù pointers, or it can have only 1 pointer to a child node.
* Calculation error. Especially: log 2 or ln 2 are not 1. Though log₂ 2 is, the 1 should not be dropped -- log (a * b) = log a + log b.

Problem 4

Let T₁ be the time taken to read one block into main memory and T₂ be the time to process that block in memory. If n blocks are examined to search for a given record, then the time taken for this search is :

n * (T₁ + T₂)

Substituting the appropriate expressions for all the variables, we get

T(m) = [ (25 + 0.02 m) + (a + b log₂m) ] * log_mN

Ignoring a in comparison with 30, we get

T(m) = [25 + 0.02 m + b log₂m] * log_mN

Substituting log₂m by ln(m)/ln(2) and log_mN by ln(N)/ln(m), we get

T(m) = [ (25 + 0.02m)/ln(m) ] * ln(N) + b * ln(N)/ln(2)

Hence, to minimize T(m), we need to minimize f(m) = (25 + 0.02m)/ln(m). A number of techniques can be applied to determine the value of m that minimizes this expression. For example, taking the derivative and setting it to zero (f'(m) = 0), we get

m * (ln (m) - 1) = 1250

This can be solved to yield an integral value of 272. It is easy to verify that this value does indeed minimize f(m) and hence T(m).

Seek+latency constant decreases : Let us split T(m) into three components as follows (here, t_s is the seek + latency time constant which was 30 in the above case) :

Total seek and latency time T_a = t_s * ln(N)/ln(m)
Total transfer time T_b = 0.02 * m * ln(N)/ln(m)
Total binary search time T_c = b * ln(N)/ln(2)

Of these, T_c is independent of m, T_a is a decreasing function of m whereas T_b is an increasing function of m. If t_s is very small, then T_a is negligible compared to T_b. Hence, we must choose a small value of m to minimize the search time. On the other hand, if T_a is very large compared to T_b, then the former dominates and we choose a large value of m to minimize search times. From these limiting cases, it is easy to see that if t_s decreases, the optimum value of m decreases. In particular, if t_s = 25/2 = 12.5, we get an optimum value of 155 (by proceeding along the same lines as above).