There are n! ways to order n relations. Each ordering gives us a different left-deep plan, because we assume all joins are asymmetric. Moreover, there are three ways to execute each join, so for each join ordering we have 3^(n-1) ways of executing the joins in the plan. Finally, there are 2 ways to execute each selection, so there are 2^n ways per ordering to execute the selections. So, the total number of plans, considering only left-deep join orders, is n!*3^(n-1)*2^n. For n=3, that gives us 432 plans.

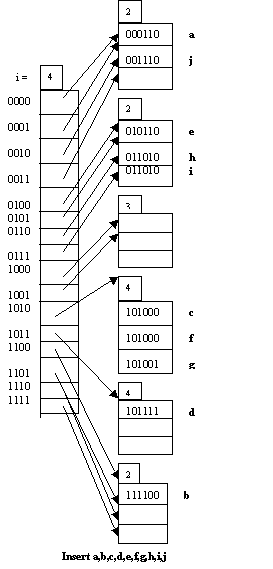
(Diagram by courtesy of Frank Luo.)
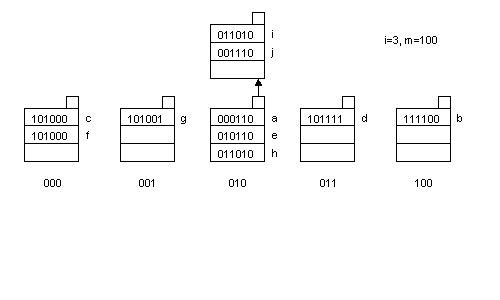
(Diagram by courtesy of Jinlin Wang.)
The purpose of this problem was to let the students think more carefully about the extensible/linear hashing schemes. If the answers were carefully thought-out, and were reasonable, they received perfect credit regardless of their conclusion.
Since the hash function randomizes the bits of the original key, it does not make any practical difference if we reverse the bits of the output hash function. More precisely, let's assume h(key) is the original hash function, and reverse(hashkey) reverses the order of the bits of hashkey. For example, reverse(0001)=1000. With these two functions, we can construct a new hash function h'(key)=reverse(hash(key)), and it practically does not make any difference whether we use h(key) or h'(key).
Using low order bits in extensible hashing or using high order bits in linear hashing is essentially the same as using h'(key) as the hash function, and as we argued above, it does not make any practical difference.