Problem 1:

a) True
Consider visiting the rows in the permuted order. The first time you see a one in any of the two columns, the column C1 \/ C2 will also have a one. Consequently, the first (minimum) row number which corresponds to the min hash value for any of the two columns will also be the min hash for C1 \/ C2.

b) False
Consider the following permuted order or rows: 1) 1 0 2) 0 1 3) 1 1 Under this permutation the minhash for C1 and C2 are 1 and 2, while that for C1 /\ C2 is 3.

c) True
Follows directly from part a)

d) True
Since h(C1) = h (C2), the first row (under the permuted order) that has a 1 in C1 also has a 1 in C2. Therefore, by definition the column C1 /\ C2 also has a 1 in this row. The result follows.

Problem 2:

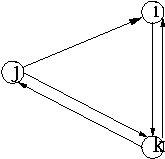
a) True
h(i) = lambda sumk A(i,k) a(k) h(j) = lambda sumk A(j,k) a(k) Out(i) subseteq Out(j) implies that whenever A(i,k) is 1, A(j,k) is also 1. This coupled with the fact that a(k)'s are positive gives the result.

b) False
Consider the following figure. In the figure Out(i) subset Out(j), while p(i) > p(j)

                                   

c) True
p(i) = (1-f)(sumk M(i,k) p(k)) + f p(j) = (1-f)(sumk M(j,k) p(k)) + f where 'f' is the fudge factor and M is the matrix that has entry M(i,k) = 1/d iff k points to i and k has degree 'd'. In(i) subseteq In(j) implies that if M(i,k) = 1/d > 0, then M(j,k) = 1/d > 0. This coupled with the fact that p(k)'s are positive gives the result

d) False
Infact the opposite is true, namely a(j) <= a(i). This follows from same reasoning as in a) with A replaced by AT and lambda replace by mu

Problem 3:

There are exactly 3 stable models: {p1,p2},{q1,p2} and {q1,q2}.  One may arrive at the answer by applying the GL-transform to all 16 candidate models but the following observations might relieve one of that tedium:
(1) Since we have pi:-NOT qi and qi:-NOT pi (for both i=1 and i=2), exactly one of pi and qi belongs in a stable model.
(2) If p1 is part of a model, then so is p2.

Observation (1) reduces the number of candidate models to check down to just 4, and observation (2) rules out the candidate {p1, q2}. The three possibilities left all turn out to be stable.

Common errors:

All errors had low support but the following two stood out:
1. Not considering all the possibilities and providing only a subset of the answer.
2. Believing that {p1,q2} is stable.

Grading:

 If the provided solution was a subset of the correct solution, your score was 15*Sim_Jaccard(Correct Solution, Your Solution).
 If you provided a superset of the correct solution, but had used Observation (1), you lost 3 points.  Otherwise, you scored min(5*#correct models in solution, 15-max(5*#wrong models in solution,10)).

Problem 4:

(a) There are 100,000-choose-2 or about 5*109 frequent pairs. These occur 100 times each, for a total of 5*1011 occurrences. The number of frequent-infreqent pairs is 1011, and these occur 10 times each, for a total of 1012 occurrences. Finally, there are 1,000,000-choose-2 or about 5*1011 infrequent pair occurrences, for a total of 2*1012 occurrences.

(b) Boy is my face red. I was imagining that pairs had to occur isolated in baskets, so one could argue just by counting the pairs in which each item participated that the support threshold had to be between 2*106 and 2*107. However, there are many other possibilities. There actually is no upper bound at all, since there could be an indefinite number of baskets with one item. For example, here's how you could explain the given data with a support threshold of one google (10100):

  1. One basket with all the infrequent items.
  2. 100 baskets with all the frequent items.
  3. For each pair of a frequent and an infrequent item, 10 baskets containing exactly those two items.
  4. For each frequent item, one google minus 10,000,100 baskets containing only that item.

On the other hand, I'm having trouble getting the exact lower bound at all. Here's as far as I've gotten. Suppose a collection of market-baskets was uniform, in the sense that it consists of k baskets, each with i infrequent items and f frequent items. Then we can place upper bounds on some functions of k, i, and f by counting the total number of pairs of various types. The fact that there are only 1,000,000-choose-2 infrequent-infrequent pair occurrences says that ki2/2 = 10^12/2. (note: throughout we'll use n2/2 as the approximation to n-choose-2). Similarly, the fact that there are 1012 frequent-infrequent pair occurrences says kif = 1012, and the fact that there are 1012/2 frequent-frequent pair occurrences says kf2 = 1012/2. We conclude that i = f, and k = 1012/i2. Finally, note that s, the support, must be bigger than the number of times any infrequent item occurs, which is s > ki/106, or s > 106/i.

Our apparent conclusion is that i should be as large as possible, which is 100,000. The reason is that i = f, and there are only 100,000 frequent items. that gives s = 11, and there were actually 4 people who gave 11 as the lower bound. However, unless someone can take this one step further, I declined to give them extra credit for that answer. The reason is that I doubt we can get specific baskets that meet all the conditions.

To begin, we could divide the 106 infrequent items into 10 groups of 100,000, and create one basket with each group and all the frequent items. However, k = 1012/i2, so we need another 90 baskets, each with 100,000 infrequent items. We cannot completely avoid reusing some of the pairs of infrequent items from the original ten groups, so we violate the condition that each pair of infrequent items appears exactly once. If we lower i, there is hope we could arrange the infrequent items into groups of i so that no pair appears more than once. There is also the option to have some baskets with one infrequent item and many frequent items, which gives us further flexibility. Anyway --- if anybody has some thoughts about the best design of the baskets, please let me know.

Given the state of this part of the problem, I decided to give everyone credit, and to ignore the problem completely.

(c) The answer is simply the answer to (a) divided by 107, or 200,000.

Common errors:

4A: Forgetting that the number of pairs of n items is n-choose-2, not N2. (-2)

4B: Omitting the frequent pairs in the calculation of (c). Note that the given support 107 is so large, that the frequent pairs distribute essentially randomly in buckets, just like the infrequent pairs. (-2)

Problem 5:

(a)

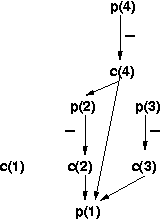
Round 0
 Round 1
 Round 2
 Round 3
 Truth Value
p(1)
 0
 0
 0
 0
 False
p(2)
 0
 1
 1
 1
 True
p(3)
 0
 1
 1
 1
 True
p(4)
 0
 1
 0
 0
 False
c(1)
 0
 0
 0
 0
 False
c(2)
 0
 0
 0
 0
 False
c(3)
 0
 0
 0
 0
 False
c(4)
 0
 1
 1
 1
 True

 
(b)
                           


(c) Stratum 0: { p(1), c(1),c(2), c(3)} Stratum 1: {p(2),p(3),c(4)} Stratum 2: {p(4)}

(d)  The program+EDB is locally stratified for all values of n.  The only negative arcs in the dependency graph are from p(x) to c(x). Since, all arcs from c(x) are to a p(y) where y<x, there can be no cycles (and, consequently, no cycles with negative arcs) in the dependency graph.  Therefore, the program+EDB is locally stratified.

Common Errors:

1.Forgetting to make inferences from positive facts derived in a round. Specifically, when you infer  p(2) to be true in Round 1, you need to use the rule c(4):-p(2) to infer that c(4) is true.  (-1)

2.The singular form of "strata" is "stratum". (-0)

Grading: 

Each part carries 4 points. You lose one point for each mistake (but you aren't docked points for cascading errors). An incorrect explanation in part (d) costs you 2 points.


Problem 6:

(a) When we expand, we get: 

q(A,B,C,D) :- e(A,B) & e(B,C) & e(A,C) & e(B,C) & e(C,D) & e(B,D)

In all expansions, A, B, C, and D from the query have to map to themselves, because they appear in the head, in that order, in both the query and solutions. In this case, e(A,D) from the query has to map to some subgoal in the expansion above, but there is no such subgoal. Hence, "solution" (a) is not contained in the query, and is not a solution.

(b) Here, the expansion is: 

q(A,B,C,D) :- e(A,B) & e(B,C) & e(A,C) & e(B,C) & e(C,D) & e(B,D) &
              e(A,C) & e(C,D) & e(A,D)

Now, there is a target for each of the 6 query subgoals, so we have a solution. It is also minimal, because if we eliminate any of the three views, since there is a common e-subgoal in the expansions of any two of these views, only five of the six query subgoals could be covered.

(c) This is also a minimal solution. The expansion is: 

q(A,B,C,D) :- e(A,B) & e(B,C) & e(A,C) & e(A,E) & e(E,D) & e(A,D) &
              e(B,F) & e(F,D) & e(B,D) & e(G,C) & e(C,D) & e(G,D)

The identity map again shows this expansion is contained in the query. Since the subgoals of the expansion that have E, F, or G are useless as the possible target of a query subgoal, we see that there are only six subgoals of the expansion that could be a target. Thus, if we remove any view-subgoal from the proposed solution, we cannot cover the query, which proves we have a minimal solution.

(d) Another minimal solution, with expansion: 

q(A,B,C,D) :- e(A,B) & e(B,C) & e(A,C) & e(B,C) & e(C,D) & e(B,D) &
              e(B,A) & e(A,D) & e(B,D)

A subgoal from the expansion of each of the three view subgoals is needed, so we cannot eliminate any view subgoals. Specifically, e(A,B) comes only from v(A,B,C), e(C,D) comes only from v(B,C,D), and e(A,D) comes only from v(B,A,D).

Common error:

6A: A number of people thought that the LMSS theorem said the number of subgoals in the expansion could not exceed the number of subgoals in the query. Rather, it is the number of subgoals in the solution before expansion that cannot exceed the number in the query. You lost 6 points if this affected your answer to more than one part. In some cases, people lost only 4 points, if for some reason this (false) theorem was invoked only once.

Problem 7:

Consider any set of three items (A,B,C) All pairs of items are frequent and hence (A,B), (B,C) and (A,C) are frequent in the sample. Hence, by definition (A,B,C) is in negative border. Consider any item set with 4 or more items. No item set with 3 items or more is frequent in the sample. Hence, no item set with 4 or more items will be part of the negative border. In other words, the negative border is exactly all the triples of items. Number of triples = 10*9*8/1*2*3 = 120

Common errors:

7A: incorrect calculation of number of triples out of 10 or not calculating them at all. (-4)

7B: having all pairs as part of the negative border (-8)

7C: no explanation (-8)

Problem 8:

(a) 

Q2: panic :- a(X,Y) & a(U,V) & X<Y & X=V & Y=U
Q1: panic :- a(A,B) & a(C,D) & A!=B & A=D & B=C

(b)

X->A; Y->B; U->A; V->B
X->A; Y->B; U->C; V->D
X->C; Y->D; U->A; V->B
X->C; Y->D; U->C; V->D

(c) 

A!=B & A=D & B=C => A<B & A=B & A=B OR
                    A<B & A=D & B=C OR
                    C<D & A=D & B=C OR
                    C<D & C=D & C=D

(d) 

A!=B & A=D & B=C => (A<B OR B<A) & A=D & B=C
     => A<B & A=D & B=C OR B<A & A=D & B=C
     => A<B & A=D & B=C OR C<D & A=D & B=C
     => entire right side of (c)

Common errors:

8A: In part (d), using "backwards" logic. That is, a common mistake was to use the left side of (c) to derive something true like "A<B OR B<A" from the right side and then declare that because the right side derives truth, it must itself be true. That's not correct. For example, I can prove from "2+2=5" that "5=5." Just because my conclusion is true doesn't mean I started with a true statement. (-2)

8B: In (b), a number of people omitted the two containment mappings that send both relational subgoals of Q2 to the same subgoal. (-2)

Problem 9:

a) True.
Since the Web graph is undirected, A = AT. Thus AAT = ATA and hence we get that h and a vectors are identical and satisfy h = lambda mu AAT h

b) False.
The following simple example of an undirected graph has M(2,1) != M(1,2)

                                 

Common errors:

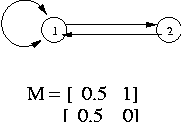
9A: for the pagerank matrix M[i,j], claiming that M[i,j] =1 whenever there is a link from j to i, or just claiming that M[i,j] = M[j,i] without explanation. (-5)

9B: little or no explanation for the hubbiness and authority problem. (-5)