Although Lemma 5.1 suggests a method of
distributing the cost of an annotated edge cover (and thus an edit
script) over the component edges, the cost of each edge depends on the
other edges present in the edge cover, and is thus not directly useful
for computing a minimum-cost edge cover. However, we use that
distribution scheme to derive upper and lower bounds on the fair cost
of an edge e over all minimal edge covers K.
Intuitively, given that the cost of any UPD annotation on an edge is
charged to that edge (by Equation 1), a
simple choice for the lower bound on the cost of an edge [m, n] is
simply the cost 
of updating the label m to that of n.
However, we can do a little better. In some cases, selecting an edge
[m, n] (as part of the edge cover being constructed) may
force some of the children m' of m to be moved to n. In
particular, this happens for those children of m' for which there is
no edge that could possibly match m' to a child of n. We call
such moves forced moves. In cases where we can determine a
forced move exists, the cost of a MOV is added to the lower bound
cost. However, according to Equation 1 not
all the cost of a forced move goes to edge [m, n]. In the worst
case, the number of edges incident on m, |E(m)|, is large, leaving
[m, n] with an insignificant contribution. However, if |E(m)| is
greater than 1, we know by Lemma 4.1 that |E(n)|=1, so
forced moves on the n side would contribute to [m, n]. Thus, we
may add the minimum of the second and the third terms in
Equation 1 to the lower bound function.
Formally, let E be the set of edges in the induced graph of 
and 
.
We define
the forced move cost, 
of a node 
with respect to another node 
as follows: 
, if 
such that 
, and 0 otherwise. The cost 
is defined
analogously. We then define the lower bound fair cost,
, of an edge as follows:
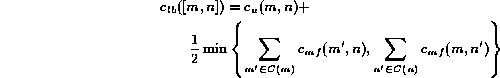
To help us compute the upper bound, let us now define a
conditional move cost, 
. Intuitively, 
costs one MOV cost unless there is a partner of m' that is a child
of n. Formally, 
, if 
such that , and 
otherwise. The cost
is defined analogously. Furthermore, define 
if m and n are regular nodes, 0 if 
, 
if 
, and 
if 
.
Using reasoning similar to that used for deriving the lower bound cost
above, we arrive at the following definition for the upper bound
fair cost, 
, of an edge:
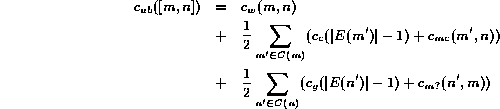
Note that both 
and 
can be computed by MH-DIFF
without knowing the target cover. Furthermore, the following lemma,
proved in [&make_named_href('',
"node21.html#bbdiffExtended","[CGM97]")], states that the above definitions
of and , are upper and lower bounds,
respectively, on the fair cost contribution of edge e to
any minimal edge cover K that contains e.
