We noted earlier that many of the potential edge covers of the induced graph are undesirable because they correspond to expensive and undesirable edit scripts. Intuitively, we may therefore expect a substantial number of the edges of the induced graph to be extraneous. Our next step, therefore, consists of removing (pruning) as many of these extraneous edges as possible from the induced graph, by using some pruning rules. The pruning rules that we use are conservative, meaning that they remove only those edges that we can be sure are not needed by a minimum-cost edit script. We discuss pruning rules in detail in Section 5.3, presenting only a simple example here.
As an example of the action of a simple pruning rule, consider the
edge 
, representing the correspondence between nodes 5
and 53 in Figure 2. Suppose that the cost
of updating the label a of node 5 to the label ac of
node 53 is 3 units. Furthermore, let the cost of inserting a node and
deleting a node be 1 unit each. Then we can safely prune the edge [5,
53] because, intuitively, given any edge cover 
that includes
the edge 
, we can generate another edge cover that excludes
, and that corresponds to an edit script that is at least as good
as the one corresponding to . As an illustration of such pruning,
consider the edge cover 
. This edge cover corresponds to an edit script
that deletes the node 5, and inserts the node 53. These two
operations cost a total of 2 units, which is less than the cost of the
update operation suggested by the edge e in edge cover . We
therefore conclude that the edge [5, 53] in our running example may
safely be pruned. In Section 5.3 we present
Pruning Rule 2, which is a generalization of this example.
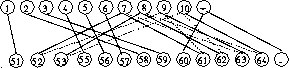
Figure: The pruned induced graph for the trees in
Figure 2