Sequential Software Engineering Methodology

 

In this section, a family of theorems are presented that pertain to the sequential software engineering methodology. The sequential software engineering methodology will find solutions in static environments but not in dynamic environments. If a solution exists, and the sequential software engineering methodology finds the solution, the best case performance is O(N), the worst case performance is O(N), while the average case performance is O(N) where N is the total number of steps in the environment.

   

Theorem 2 (Sequential: Static Complete)   A sequential software engineering methodology is static complete.  

Let $a_1, a_2, a_3, \ldots, a_{n{_a}}$ be the n_a requirements leading to a possible analysis A with a₁ the initial problem statement. Let $d_1, d_2, d_3, \ldots, d_{n{_d}}$ be the n_d architecture elements leading to a possible design D. Let $i_1, i_2, i_3, \ldots, i_{n{_i}}$ be the n_i implementation components leading to a possible implementation I. Let $t_1, t_2, t_3, \ldots, t_{n{_t}}$ be the n_t testing suites leading to a possible testing T with t_nt being the final system acceptance test. Define a static environment that consists of the four planes of analysis, design, implementation, and testing with each lower plane being a refinement of the higher planes. Define the solution as the tree, or in a more general sense, the directed acyclic graph, of all steps from all four planes used in the final system. This solution can be represented as a sequence of steps <A,D,I,T>.

See Figure 5.5 on page for a visual representation of the static environment. See Figure 5.9, Figure 5.10, and Figure 5.11, on pages through for a visual guide of the reasoning. The numbers associated with the steps represent the order visited by the methodology.

  

Figure 5.9: Sequential: Beginning

  

Figure 5.10: Sequential: Intermediate

  

Figure 5.11: Sequential: Final

Proof 2.1  

A sequential software engineering methodology leads to a sequence of steps.

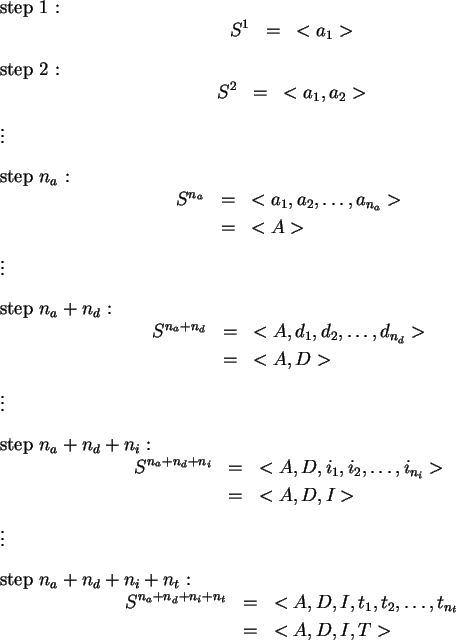
The sequence represented by <A,D,I,T> is the solution.

These steps find a solution where steps at the higher levels are exhausted first before going into lower levels. If the environment is static, then all steps in the environment are known before the sequential methodology begins. The sequential methodology first discovers all steps in the analysis plane, followed by all steps in the design plane, followed by all steps in the implementation plane, and then followed by all steps in the testing plane. This can be accomplished because the environment is static and finite. Eventually in the static environment the solution is discovered. Thus, the sequential software engineering methodology is static complete.

   

Corollary 2.1 (Sequential: Best Case)   The best case performance of the sequential software engineering methodology is O(N).  

Proof 2.1.1   Let the environment consist of n_a analysis steps, n_d design steps, n_i implementation steps, and n_t testing steps. Let the system acceptance test be the very fist step in the testing plane t₁. The number of steps to find a solution is n_a + n_d + n_i + 1 which is O(N).

   

Corollary 2.2 (Sequential: Worst Case)   The worst case performance of the sequential software engineering methodology is O(N) where N is the size of the space.  

Proof 2.2.1   Let the environment consist of n_a analysis steps, n_d design steps, n_i implementation steps, and n_t testing steps. Let the system acceptance test be the very last step t_n<<1790>>t. The number of steps to find a solution is n_a + n_d + n_i + n_t which is O(N).

   

Corollary 2.3 (Sequential: Average Case)   The average case performance of the sequential software engineering methodology is O(N) where N is the size of the space.  

Proof 2.3.1   Let the environment consist of n_a analysis steps, n_d design steps, n_i implementation steps, and n_t testing steps. Let the system acceptance test be the (n_t)/2 step in the testing plane t_(nt)/2. The number of steps to find a solution is n_a + n_d + n_i + (n_t)/2 which is O(N).

   

Corollary 2.4 (Sequential: Dynamic Incomplete)   The sequential software engineering methodology may not find a solution in a dynamic environment.  

In a sequential software engineering methodology, all of the high level steps are exercised before proceeding to the next plane of the space. If a new step is introduced once the sequential software engineering methodology has finished with this plane of the environment, the new step will not be part of the solution. The sequential methodology will no longer be able to find the solution.

Let the initial environment consist of n_a analysis steps, n_d design steps, n_i implementation steps, and n_t testing steps.

Proof 2.4.1  

At step n_a + 1 the sequential software engineering methodology has accomplished the steps $<a_1, a_2, \ldots, a_{n_{a}}, d_1>$. At this time introduce a new requirement a_n<<1807>>a+1. The sequential software engineering methodology has already finished with the analysis plane and will not discover this new requirement. Thus, a sequential software engineering methodology is dynamic incomplete.

   

Corollary 2.5 (Sequential: Non-monotonic Incomplete)   The sequential software engineering methodology may not find a solution in a non-monotonic environment.  

Proof 2.5.1   The sequential software engineering methodology is incomplete in dynamic environment and thus incomplete to dynamic environments with the non-monotonic property.