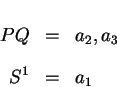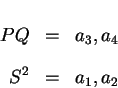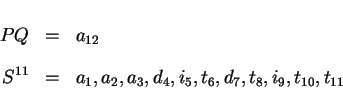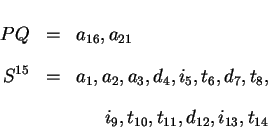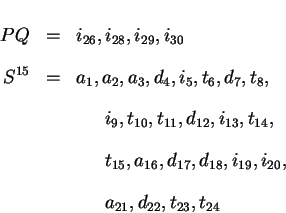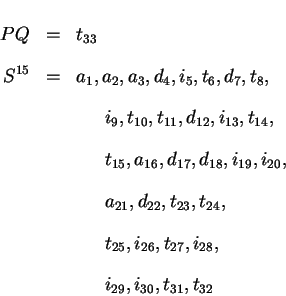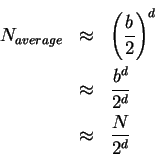Next: Summary Results from the
Up: Supporting Theorems
Previous: An Example of Cyclical
In this section, a family of theorems are presented that pertain to the WaterSluice software engineering methodology.
The WaterSluice software engineering methodology will find solutions in static environments and dynamic environments including dynamic environments that
have the non-monotonic property. If a solution exists and the
WaterSluice software engineering methodology finds the solution, the best case performance is O(1), the
worst case performance is O(N), while the
average case performance is an order-of-magnitude less than N where N is the total number of steps in the environment.
Theorem 4 (WaterSluice: Static Complete)
The WaterSluice software engineering methodology is static complete.
Let
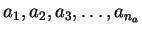 be the na steps
leading to the possible analysis A with a1 being the
initial problem statement.
Let
be the na steps
leading to the possible analysis A with a1 being the
initial problem statement.
Let
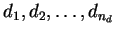 be the nd steps
leading to the possible design D.
Let
be the nd steps
leading to the possible design D.
Let
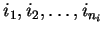 be the ni steps leading
to the possible implementation I.
Let
be the ni steps leading
to the possible implementation I.
Let
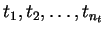 be the nt steps leading
to the possible testing T
with tn<<1931>>4 being the
final system acceptance
test.
Define an environment that consists of the four planes of analysis, design, implementation, and testing with each lower plane being a refinement of the higher planes.
In this environment priorities are represented
as different in the size of a step. A larger circle represents a higher priority than a smaller circle.
Define the solution as the tree, or in a more general sense,
the directed acyclic graph, of all steps from all four planes
used in the final system.
Define a priority queue of possible next steps PQ. Initially the
priority queue PQ contains the initial step a1
represented by the sequence S1.
Define a function, next, over all possible steps,
which generates all possible next steps given the current solution sequence,
evaluates the total value, and pushes the ordered result onto the priority queue PQ. Only high priority steps are
keep in the queue PQ.
See Figure 5.13 on page
be the nt steps leading
to the possible testing T
with tn<<1931>>4 being the
final system acceptance
test.
Define an environment that consists of the four planes of analysis, design, implementation, and testing with each lower plane being a refinement of the higher planes.
In this environment priorities are represented
as different in the size of a step. A larger circle represents a higher priority than a smaller circle.
Define the solution as the tree, or in a more general sense,
the directed acyclic graph, of all steps from all four planes
used in the final system.
Define a priority queue of possible next steps PQ. Initially the
priority queue PQ contains the initial step a1
represented by the sequence S1.
Define a function, next, over all possible steps,
which generates all possible next steps given the current solution sequence,
evaluates the total value, and pushes the ordered result onto the priority queue PQ. Only high priority steps are
keep in the queue PQ.
See Figure 5.13 on page ![[*]](cross_ref_motif.gif) for a visual representation of the space.
Here a larger circle represents a higher priority step.
See figures 5.13,
5.15,
5.16,
5.17, and
5.18
on pages
for a visual representation of the space.
Here a larger circle represents a higher priority step.
See figures 5.13,
5.15,
5.16,
5.17, and
5.18
on pages ![[*]](cross_ref_motif.gif) through
through
![[*]](cross_ref_motif.gif) for a visual guide of the reasoning.
The numbers associated with the steps represent the order
visited by the methodology.
for a visual guide of the reasoning.
The numbers associated with the steps represent the order
visited by the methodology.
Figure 5.13:
Priority Based Space
|
|
Figure 5.14:
WaterSluice: Proof of Principle
|
|
Figure 5.15:
WaterSluice: Prototype
|
|
Figure 5.16:
WaterSluice: Alpha
|
|
Figure 5.17:
WaterSluice: Beta
|
|
Figure 5.18:
WaterSluice: Product
|
|
Proof 4.1
The WaterSluice methodology leads to this sequence
of steps.
- step 1: Initial set up.
PQ & = & a1
- step 2: Remove a1 from the priority queue PQ. Expand all alternative steps near a1 using
the function next and push them onto the priority queue PQ.
At this stage there are two alternative next steps. Pick the
next step with the highest priority.
For clarity, assume this step is
a2.
- step 3:
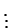
- step 11:
The methodology is now at the proof of principle stage.
- step 15:
The methodology is now at the prototype stage.
- step 24:
The methodology is now at the alpha stage.
- step 32:
The methodology is now at the beta stage.
- step
na + nd + ni + nt:
The priority queue contains the last step of the final system acceptance test.
Thus, the WaterSluice software engineering methodology is static complete.
The WaterSluice software engineering methodology uses priority to guide the process combined with the iterative mechanism found in a cyclical methodology and governed by the steady progression found in a sequential methodology.
If the environment is static, then all steps in the environment are known before the WaterSluice software engineering methodology begins.
The WaterSluice software engineering methodology first discovers high priority steps from the analysis plane, the design plane, the implementation plane, and the testing plane.
As higher priority steps are discovered and visited, they
are eventually exhausted. This allows the lower
priority steps to be visited.
The WaterSluice software engineering methodology
continues until the only remaining step to visit is the lowest possible priority step.
Corollary 4.1 (WaterSluice: Dynamic Complete)
The WaterSluice software engineering methodology is dynamic complete.
Proof 4.1.1
The WaterSluice software engineering methodology allows for the introduction of new information at every step and the removal of information that is no longer needed.
Recall the presence of the priority queue. When steps are placed on the priority queue, the queue is rearranged. Low priority steps migrate to the end of the queue while high priority steps migrate to the beginning of the queue.
Regardless of when a high priority item
is discovered, the methodology will be able to react.
For a dynamic environment, the WaterSluice software engineering methodology will eventually find the solution.
Corollary 4.2 (WaterSluice: Non-monotonic Complete)
The WaterSluice software engineering methodology is non-monotonic complete.
Proof 4.2.1
The WaterSluice software engineering methodology allows for the introduction of new information at every step and the removal of information that is no longer needed.
Define a priority function that takes into account non-monotonic steps. Consistent steps are assigned similar high priority. Non-consistent steps are assigned lower priority.
When steps are placed on the priority queue, the queue is rearranged. Low priority steps migrate to the end of the queue while high priority steps migrate to the beginning of the queue.
Regardless of when a high priority item
is discovered, the methodology will be able to react.
For a non-monotonic space, the WaterSluice software engineering methodology will eventually find the solution leaving behind the conflicting steps.
Corollary 4.3 (WaterSluice: Best Case)
The best case performance of the WaterSluice software engineering methodology is O(1).
Proof 4.3.1
Let the environment consist of
na analysis steps, nd design steps, ni implementation steps, and nt testing steps.
Let the correct analysis step be the very first step
a1.
Let the correct design step be the very first step
d1.
Let the correct implementation step be the very first step
i1.
Let the system acceptance test be the very first step t1.
To satisfy the problem statement would
require one analysis, one design, one implementation, and one testing step.
In this environment the WaterSluice software engineering methodology will require only four steps. Thus the performance is O(1).
Corollary 4.4 (WaterSluice: Worst Case)
The worst case performance of the WaterSluice software engineering methodology is O(N) where N is the size of the environment.
Proof 4.4.1
Let the environment consist of
na analysis steps, nd design steps, ni implementation steps, and nt testing steps.
Let the system acceptance test be the lowest priority step tn<<2119>>t. The number of steps to find a solution is
na + nd + ni + nt which is O(N).
Corollary 4.5 (WaterSluice: Average Case)
The average case performance of the WaterSluice software engineering methodology is
an order-of-magnitude less than N where N is the size of the environment.
Proof 4.5.1
Let d be the depth of the space. In the special case
of this space d is 4.
Let b be the average fan out of a step in the space if there
was no priority function.
If the space has N steps then
To a reasonable approximation, only the last term is
significant and
Consider the addition of a priority function. The best case
priority function would guide the algorithm directly to
a solution. In this case, the fan out would be 1 and the
total number of steps would be O(1). A worst case
priority function would not guide the algorithm. Thus
the fan out would be b and the total number of steps
would be O(N). In the average case, the priority function would trim the fan out by half. Thus
On average the performance of the algorithm is an order-of-magnitude less
than N.
Table 5.1:
Summary of Completeness
| Methodology |
Static Complete |
Dynamic Complete |
Non-monotonic Complete |
|
| sequential |
yes |
no |
no |
|
| cyclical |
yes |
yes |
no |
|
| WaterSluice |
yes |
yes |
yes |
|
|
Table 5.2:
Summary of Performance
| Methodology |
Best |
Worst |
Average |
|
| sequential |
O(N) |
O(N) |
O(N) |
|
| cyclical |
O(1) |
O(N) |
O(N) |
|
| WaterSluice |
O(1) |
O(N) |
order-of-magnitude less than N |
|
|



Next: Summary Results from the
Up: Supporting Theorems
Previous: An Example of Cyclical
Ronald LeRoi Burback
1998-12-14
![[*]](cross_ref_motif.gif) for a visual representation of the space.
Here a larger circle represents a higher priority step.
See figures 5.13,
5.15,
5.16,
5.17, and
5.18
on pages
for a visual representation of the space.
Here a larger circle represents a higher priority step.
See figures 5.13,
5.15,
5.16,
5.17, and
5.18
on pages ![[*]](cross_ref_motif.gif) through
through
![[*]](cross_ref_motif.gif) for a visual guide of the reasoning.
The numbers associated with the steps represent the order
visited by the methodology.
for a visual guide of the reasoning.
The numbers associated with the steps represent the order
visited by the methodology.
![\resizebox{\textwidth}{!}{\includegraphics[bb=35 36 756 577,height=10.014in,width=7.5in]{mf12.eps}}](img44.gif)
![\resizebox{\textwidth}{!}{\includegraphics[bb=35 36 756 577,height=10.014in,width=7.5in]{psearch1.eps}}](img45.gif)
![\resizebox{\textwidth}{!}{\includegraphics[bb=35 36 756 577,height=10.014in,width=7.5in]{psearch2.eps}}](img46.gif)
![\resizebox{\textwidth}{!}{\includegraphics[bb=35 36 756 577,height=10.014in,width=7.5in]{psearch3.eps}}](img47.gif)
![\resizebox{\textwidth}{!}{\includegraphics[bb=35 36 756 577,height=10.014in,width=7.5in]{psearch4.eps}}](img48.gif)
![\resizebox{\textwidth}{!}{\includegraphics[bb=35 36 756 577,height=10.014in,width=7.5in]{psearch5.eps}}](img49.gif)