In this section, we describe our implementation of MH-DIFF, and
discuss its analytical and empirical performance.
Figure 9 depicts the overall architecture of our
implementation, with rectangles representing the modules (numbered,
for reference) of the program, and other shapes representing data.
Given two trees 
and 
as input, Module 1 constructs the
induced graph (Section 3.1). This induced graph
is next pruned (Module 2) using the pruning rules of
Section 5.3 to give the pruned induced graph. In
Module 2, the update cost for each edge in the induced graph is
computed using the domain-dependent comparison function for node
labels (Section 2.2). The next three modules
together compute a minimum-cost edge cover of the pruned induced graph
using the reduction of the edge cover problem to a weighted matching
problem [&make_named_href('',
"node21.html#combopt","[PS82]")]. That is, the pruned induced graph is first
translated (by Module 3) into an instance of a weighted matching
problem. This weighted matching problem is solved using a package
(Module 4) [&make_named_href('',
"node21.html#wmatch","[Rot]")] based on standard techniques [&make_named_href('',
"node21.html#combopt","[PS82]")].
The output of the weighted matching solver is a minimum-cost matching,
which is translated by Module 5 into 
, a minimum-cost edge cover
of the pruned induced graph. Next, Module 6 uses the minimum-cost
edge cover computed, to produce the desired edit script, using the
method described in Section 4.2).
Recall that since we use a heuristic cost function to compute a
minimum-cost edge cover, the edge cover produced by our program, and
hence the edit script may not be the optimal one. We have also
implemented a simple search module that starts with minimum-cost edge
cover (see Figure 9) computed by our
program and explores its neighborhood of minimal edge covers in an
effort to find a better solution. The search proceeds by first
exploring minimal edge covers that contain only one edge not in .
Next, we explore minimal edge covers containing two edges not in
, and so on. The intuition is that we expect the optimal
solution to be ``close'' to the initial solution . Although, in
the worst case, such an exploration may be extremely time-consuming,
note that as a result of pruning edges, the search space is typically
much smaller than the worst case. Due to space constraints, we do not
describe the details of this search phase in this paper.
We have used our implementation to compute the differences between
query results as part of the Tsimmis and 
projects at Stanford
[&make_named_href('',
"node21.html#TsimmisOverview","[CGMH 
94]"), &make_named_href('',
"node21.html#c3","[WU95]")]. These projects use the OEM data model,
which is a simple labeled-object model to represent tree-structured
query results. In particular, we have run our system on the output of
Tsimmis queries over a bibliographic information source that contains
information about database-related publications in a format similar to
BibTeX. Since the data in this information source is mainly textual,
we treat all labels as strings. For the domain-dependent label-update
cost function, we use a weighted character-frequency histogram
difference scheme that compares strings based on the number of
occurrences of each character of the alphabet in them. For example,
consider comparing the labels ``foobar'' and ``crowbar.'' The
character-frequency histograms are, respectively, 
and 
. The difference histogram is 
. Adding up the magnitudes of
the differences gives us 5, which we then normalize by the total
number of characters in the strings (13), and scale by a parameter
(currently 5), to get the update cost (5/13)*5 = 1.9 .
Let us now analyze the running time of our program. Let n be the
total number of nodes in both input trees and .
Constructing the induced graph (Module 1, in
Figure 9) involves building a complete bipartite
graph with O(n) nodes on each side. We also evaluate the
domain-dependent label-comparison function for each pair of nodes, and
store this cost on the corresponding edge. Thus, building the induced
graph requires time 
, where k is the cost of the
domain-dependent comparison function. Next, consider the pruning phase
(Module 2). By maintaining a priority queue (based on edge costs) of
edges incident on each node of the induced graph, the test to
determine whether an edge may be pruned can be performed in constant
time. If the edge is pruned, removing it from the induced graph
requires constant time, while removing it from the priority queues at
each of its nodes requires O(log n) time. When an edge [m,n]
is pruned, we also record the changes to the costs 
, 
, 
, and 
,
which can be done in constant time. Thus, pruning an edge requires
O(log n) time. Since at most 
are pruned, the total worst
case cost of the pruning phase is 
. Let e be the
number of edges that remain in the induced graph after pruning. The
minimum-cost edge cover is computed in time O(ne) by Modules 3, 4,
and 5. The computation of the edit script from the minimum-cost edge
cover can be done in O(n) time by Module 6. (Note that the number
of edges in a minimal edge cover is always O(n) .)
The number of edges that remain in the induced graph after pruning (denoted by e above) is an important metric for three main reasons. Firstly, as seen above, a lower number of edges results in faster execution of the minimum-cost edge cover algorithm. Secondly, a smaller number of edges decreases the possibility of finding a suboptimal edge cover, since there are fewer choices that need to be made by the algorithm. Thirdly, having a smaller number of edges in the induced graph reduces exponentially the size of the space of candidate minimal edge covers that the search module needs to explore.
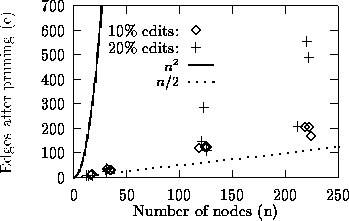
Figure 10: Effectiveness of pruning
Given the importance of the metric e, we have conducted a number of
experiments to study the relationship between e and n. We start
with four ``input'' trees representing actual results of varying sizes
from our Tsimmis system. For each input tree, we generate a batch of
``output'' trees by applying a number of random edits. The number of
random edits is either 10% or 20% of the number of nodes in the
input tree. Then for each output tree, we run MH-DIFF on it and its
original input tree. The results are summarized by the graph in
Figure 10. The horizontal axis indicates the total
number of nodes in the two trees being compared (and hence, in the
induced graph). The vertical axis indicates the number of edges that
remain after pruning the induced graph. Note that the ideal case
(best possible pruning) corresponds to 
,
since we need at least 
edges to cover n nodes,
whereas the worst case is 
(no pruning at all). For
comparison, we have also plotted e = n/2 and on the
graph in Figure 10. We observe that the relationship
between e and n is close to linear, and that the observed values
of e are much closer to n/2 than to 
.
Note that in Figure 10 we have plotted the results for two different values of d, the percentage of random edit operations applied to the input tree. We see that, for a given value of n, a higher value of d results in a higher value of e, in general. We note that some points with a higher d value seem to have a lower value of e than the general trend. This is because applying d random edits is not the same as having the input and output trees separated by d edits, due to the possibility of redundant edit operations. Thus, some data points, even though they were obtained by applying d random edits, actually correspond to fewer changes in the tree.
We have also studied the quality of the initial solution produced by
MH-DIFF. In particular, we are interested in finding out in what
fraction of cases our method produces suboptimal initial solutions,
and by how much the cost of the suboptimal solution exceeds that of
the optimal. Given the exponential (in e) size of the search space
of minimal edge covers of the induced graph, it is not feasible to try
exhaustive searches on large datasets. However, we have exhaustively
searched the space of minimal edge covers, and corresponding edit
scripts, for smaller datasets. We ran 50 experiments, starting with
an input tree derived as in the experiments for e above, and
using 6 randomly generated edit operations to generate an output
tree.
We searched the space of minimal
edge covers of the pruned induced graph exhaustively for these cases,
and found that the MH-DIFF initial solution differed from the
minimum-cost one in only 2 cases out of 50. That is, in 96% of the
cases MH-DIFF found the minimum cost edit script, and of course it did
this in much less time than the exhaustive method. In the two cases
where MH-DIFF missed, the resulting script cost about 15% more that
the minimum cost possible.
