


Next: Edit Scripts
Up: Overview and Preliminaries
Previous: Overview and Preliminaries
In an ordered tree, if nodes 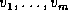 are the children of
node u, then we call
are the children of
node u, then we call 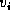 the ith child of u. For a node x,
we let
the ith child of u. For a node x,
we let 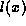 denote the label of x,
denote the label of x, 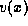 denote the value of x,
and
denote the value of x,
and 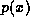 denote the parent of x if x is not the root. We assume
that labels are chosen from a fixed but arbitrary set. In the
definitions of the edit operations,
denote the parent of x if x is not the root. We assume
that labels are chosen from a fixed but arbitrary set. In the
definitions of the edit operations, 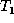 refers to the tree on
which the operation is applied, while
refers to the tree on
which the operation is applied, while 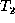 refers to the resulting
tree. The four edit operations on trees are the following:
refers to the resulting
tree. The four edit operations on trees are the following:
- Insert:
- The insertion of a new leaf node x into
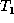 ,
denoted by
,
denoted by 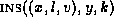 . A node x with label l and
value v is inserted as the kth child of node y of
. A node x with label l and
value v is inserted as the kth child of node y of 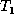 .
More precisely, if
.
More precisely, if 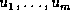 are the children of y in
are the children of y in
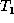 , then
, then 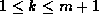 and
and 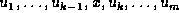 are the children of y in
are the children of y in
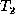 . The value v is optional, and is assumed to be null if omitted.
. The value v is optional, and is assumed to be null if omitted.
- Delete:
- The deletion of a leaf node x of
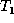 , denoted
by
, denoted
by 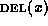 . The result
. The result 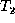 is the same as
is the same as 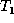 , except that it
does not contain node x.
, except that it
does not contain node x. 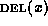 does not change the relative
ordering of the remaining children of
does not change the relative
ordering of the remaining children of 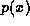 . This operation deletes only a
leaf node; to delete an interior node, we must first move its
descendents to their new locations or delete them.
. This operation deletes only a
leaf node; to delete an interior node, we must first move its
descendents to their new locations or delete them.
- Update:
-
The update of the value of a node x in
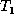 , denoted by
, denoted by 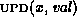 .
. 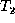 is the same as
is the same as 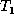 except that in
except that in 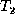 ,
,
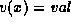 .
.
- Move:
- The move of a subtree from one parent to another in
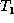 , denoted by
, denoted by 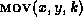 .
. 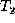 is the same as
is the same as 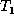 ,
except x becomes the kth child of y. The entire subtree
rooted at x is moved along with x.
,
except x becomes the kth child of y. The entire subtree
rooted at x is moved along with x.
Figure 2 shows examples of edit operations on
trees. In the figure, node 6 has label A and value foo. The labels and
values of the other nodes are not shown.
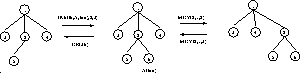
: Edit operations on a tree



Next: Edit Scripts
Up: Overview and Preliminaries
Previous: Overview and Preliminaries
Sudarshan S. Chawathe
Wed Jun 19 08:22:34 PDT 1996
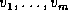 are the children of
node u, then we call
are the children of
node u, then we call 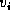 the ith child of u. For a node x,
we let
the ith child of u. For a node x,
we let 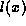 denote the label of x,
denote the label of x, 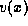 denote the value of x,
and
denote the value of x,
and 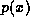 denote the parent of x if x is not the root. We assume
that labels are chosen from a fixed but arbitrary set. In the
definitions of the edit operations,
denote the parent of x if x is not the root. We assume
that labels are chosen from a fixed but arbitrary set. In the
definitions of the edit operations, 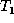 refers to the tree on
which the operation is applied, while
refers to the tree on
which the operation is applied, while 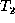 refers to the resulting
tree. The four edit operations on trees are the following:
refers to the resulting
tree. The four edit operations on trees are the following:
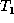 ,
denoted by
,
denoted by 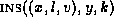 . A node x with label l and
value v is inserted as the kth child of node y of
. A node x with label l and
value v is inserted as the kth child of node y of 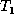 .
More precisely, if
.
More precisely, if 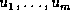 are the children of y in
are the children of y in
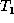 , then
, then 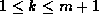 and
and 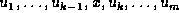 are the children of y in
are the children of y in
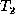 . The value v is optional, and is assumed to be null if omitted.
. The value v is optional, and is assumed to be null if omitted.
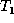 , denoted
by
, denoted
by 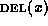 . The result
. The result 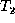 is the same as
is the same as 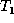 , except that it
does not contain node x.
, except that it
does not contain node x. 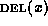 does not change the relative
ordering of the remaining children of
does not change the relative
ordering of the remaining children of 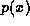 . This operation deletes only a
leaf node; to delete an interior node, we must first move its
descendents to their new locations or delete them.
. This operation deletes only a
leaf node; to delete an interior node, we must first move its
descendents to their new locations or delete them.
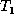 , denoted by
, denoted by 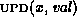 .
. 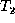 is the same as
is the same as 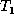 except that in
except that in 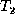 ,
,
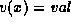 .
.
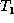 , denoted by
, denoted by 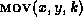 .
. 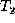 is the same as
is the same as 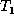 ,
except x becomes the kth child of y. The entire subtree
rooted at x is moved along with x.
,
except x becomes the kth child of y. The entire subtree
rooted at x is moved along with x.
