In this section, we formulate the change detection problem and split it into two subproblems that are discussed in later sections. We first introduce these problems informally using an example, and then present the formal definitions and terms used in the rest of the paper.
Hierarchically structured information can be represented as
ordered trees---trees in which the children of each node have a
designated order. We address our problem of detecting and
representing changes in the context of such trees. (Hereafter, when
we use the term ``tree'' we mean an ordered tree.) We consider trees
in which each node has a label and a value.![]() We also assume
that each tree node has a unique identifier; identifiers may be
generated by our algorithms when they are not provided in the data
itself. Note that the nodes that represent the same real-world entity
in different versions may not have the same identifier. We refer to
the node with identifier x as ``node x'' for conciseness.
We also assume
that each tree node has a unique identifier; identifiers may be
generated by our algorithms when they are not provided in the data
itself. Note that the nodes that represent the same real-world entity
in different versions may not have the same identifier. We refer to
the node with identifier x as ``node x'' for conciseness.
As a running example, consider trees 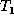 and
and 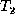 shown in
Figure 1, and ignore the dashed lines for the
moment. The number inside each node is the node's identifier and the
letter beside each node is its label. All of the interior nodes have
null values, not shown. Leaf nodes have the values indicated in
parentheses. (These trees could represent two structured documents,
where the labels D, P, and S denote Document,
Paragraph, and Sentence, respectively. The values of the
sentence nodes are the sentences themselves.) We are interested in
finding the delta between these two trees. We will assume that
shown in
Figure 1, and ignore the dashed lines for the
moment. The number inside each node is the node's identifier and the
letter beside each node is its label. All of the interior nodes have
null values, not shown. Leaf nodes have the values indicated in
parentheses. (These trees could represent two structured documents,
where the labels D, P, and S denote Document,
Paragraph, and Sentence, respectively. The values of the
sentence nodes are the sentences themselves.) We are interested in
finding the delta between these two trees. We will assume that 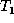 represents the ``old'' data and
represents the ``old'' data and 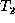 the ``new'' data, so we want to
determine an appropriate transformation from tree
the ``new'' data, so we want to
determine an appropriate transformation from tree 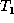 to tree
to tree 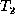 .
.
Our first task in finding such a transformation is to determine nodes
in the two trees that correspond to one another. Intuitively, these
are nodes that either remain unchanged or have their value updated in
the transformation from 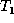 to
to 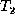 (rather than, say, deleting the
old node and inserting a new one). For example, node 5 in
(rather than, say, deleting the
old node and inserting a new one). For example, node 5 in 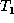 has
the same value as node 15 in
has
the same value as node 15 in 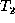 , so nodes 5 and 15 should probably
correspond. Similarly, nodes 4 and 13 have one child node each, and
the child nodes have the same value, so nodes 4 and 13 should probably
correspond. The notion of a correspondence between nodes that have
identical or similar values is formalized as a
matching between node identifiers. Matchings are one-to-one.
We say that a matching is partial if only some nodes in the two
trees participate, while a matching is total if all nodes
participate. Hereafter, we use the term ``matching'' to mean a
partial matching unless stated otherwise.
, so nodes 5 and 15 should probably
correspond. Similarly, nodes 4 and 13 have one child node each, and
the child nodes have the same value, so nodes 4 and 13 should probably
correspond. The notion of a correspondence between nodes that have
identical or similar values is formalized as a
matching between node identifiers. Matchings are one-to-one.
We say that a matching is partial if only some nodes in the two
trees participate, while a matching is total if all nodes
participate. Hereafter, we use the term ``matching'' to mean a
partial matching unless stated otherwise.
Hence, one of our problems is to find an appropriate matching for the trees we are comparing. We call this problem the Good Matching problem. In some application domains the Good Matching problem is easy, such as when data objects contain object identifiers or unique keys. In other domains, such as structured documents, the matching is based on labels and values only, so the Good Matching problem is more difficult. Furthermore, not only do we want to match nodes that are identical (with respect to the labels and values of the nodes and their children), but we also want to match nodes that are ``approximately equal.'' For instance, node 3 in Figure 1 probably should match node 14 even though node 3 is missing one of the children of 14. Details of the Good Matching problem---including what constitutes a ``good'' matching---are addressed in Section 5. A matching for our running example is illustrated by the dashed lines in Figure 1.
We say that two trees are isomorphic if they are identical
except for node identifiers. For trees 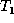 and
and 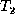 , once we have
found a good (partial) matching M, our next step is to find a
sequence of ``change operations'' that transforms tree
, once we have
found a good (partial) matching M, our next step is to find a
sequence of ``change operations'' that transforms tree 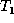 into a
tree
into a
tree 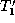 that is isomorphic to
that is isomorphic to 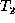 . Changes may include
inserting (leaf) nodes, deleting nodes, updating the values of nodes,
and moving nodes along with their subtrees. Intuitively, as
. Changes may include
inserting (leaf) nodes, deleting nodes, updating the values of nodes,
and moving nodes along with their subtrees. Intuitively, as 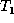 is
transformed into
is
transformed into 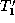 , the partial matching M is extended into a
total matching
, the partial matching M is extended into a
total matching 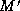 between the nodes of
between the nodes of 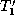 and
and 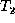 . The total
matching
. The total
matching 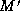 then defines the isomorphism between trees
then defines the isomorphism between trees 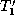 and
and
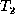 . We call the sequence of change operations an edit
script, and we say that the edit script conforms to the
original matching M provided that
. We call the sequence of change operations an edit
script, and we say that the edit script conforms to the
original matching M provided that 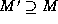 . (As will be
seen, an edit script conforms to partial matching M as long as the
script does not insert or delete nodes participating in M.) Edit
scripts are defined in more detail shortly.
. (As will be
seen, an edit script conforms to partial matching M as long as the
script does not insert or delete nodes participating in M.) Edit
scripts are defined in more detail shortly.
We would like our edit script to transform tree 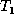 as little as
possible in order to obtain a tree isomorphic to
as little as
possible in order to obtain a tree isomorphic to 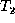 . To capture
minimality of transformations, we introduce the notion of the
cost of an edit script, and we look for a script of minimum cost.
Thus, our second main problem is the problem of finding such a minimum
cost edit script; we refer to this as the Minimum Conforming
Edit Script (MCES) problem. The remainder of this section formally
defines edit operations and edit scripts. Our algorithm for the MCES
problem is presented in Section 4, and
Section 5 presents our algorithm for the Good
Matching problem. Note that we consider the MCES problem before the
Good Matching problem, despite the fact that our method requires
finding a matching before generating an edit script. As will be seen,
the definition of a good matching relies on certain aspects of edit
scripts, so for presentation purposes we consider the details of our
edit script algorithms first.
. To capture
minimality of transformations, we introduce the notion of the
cost of an edit script, and we look for a script of minimum cost.
Thus, our second main problem is the problem of finding such a minimum
cost edit script; we refer to this as the Minimum Conforming
Edit Script (MCES) problem. The remainder of this section formally
defines edit operations and edit scripts. Our algorithm for the MCES
problem is presented in Section 4, and
Section 5 presents our algorithm for the Good
Matching problem. Note that we consider the MCES problem before the
Good Matching problem, despite the fact that our method requires
finding a matching before generating an edit script. As will be seen,
the definition of a good matching relies on certain aspects of edit
scripts, so for presentation purposes we consider the details of our
edit script algorithms first.