Returning to the pruned induced graph of our running example, let us
assume that we have gone through the process of determining the cost
of each edge, and have computed a minimum-cost edge cover according to
these costs, obtaining the edge cover represented by the bold edges in
Figure 3. Our next step consists of using this
edge cover to compute an edit script that transforms the tree 
to
the tree 
. Our algorithm CtoS (Cover-to-Script) for this
purpose is described in Section 5. Here, we
briefly illustrate some of the ideas used by the algorithm by
considering its action on an edge in the edge cover for our running
example.
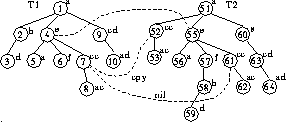
Figure: Annotating edges in the edge cover of
Figure 3
Consider the edge 
of the edge cover depicted by the
bold lines in Figure 3. In
Figure 4, we depict this edge in relation
to the original trees. (We also depict two other edges from the edge
cover. The edge cover edges are shown as dashed lines in
Figure 4. We observe that there is one
other edge in the edge cover that is incident on node 7, viz. [7,
61] , suggesting that the node 7 was copied either directly, or
indirectly (due to one of its ancestors being copied). Furthermore,
we note that the parent (node 4) of node 7 is matched to the parent
(node 55) of node 61 (i.e., the edge [4, 55] exists in the edge
cover), while the parent of node 52 is not matched to the
parent of node 7. This matching of the parents suggests that node 61
is the original instance of node 7, while node 52 is the copy. We
therefore generate a copy operation that copies the subtree rooted at
node 7 to the location of node 52. A convenient way of depicting this
copy operation is by annotating the corresponding edge ( [7,
52] in our example) with a CPY mark; this scheme allows us to talk
about edit operations without having to refer to explicit node
identifiers. Edges that do not correspond to any edit operation
(e.g., [ 6, 57 ] in our example) are annotated with a NIL mark.
In the sequel, we will use such edge annotations interchangeably with
the actual edit operations that they represent.
Consider next the edges [8, 53] and [8, 62]. Although both these
edge cover edges are incident on node 8, neither of them corresponds
to a CPY operation, since the copy 52 of node 8 is generated ``for
free'' when node 7 is copied. Therefore, both these edges are
annotated NIL. Proceeding thusly, we annotate all the edges in the
edge cover of our running example, to obtain the annotated edge cover
depicted in Figure 5, which shows only the
edges with non-nil annotations, for clarity. These annotations
correspond to the edit script
. We see that this edit script is identical to the one
in Example 2.1, which happens to be a minimum cost
edit script for our example. Of course, the above edit operations may
also be listed in the order 
. Both edit scripts have the same final effect, and have the same
cost. In general, all edit scripts corresponding to a set of
annotated edges have the same overall effect and the same cost.
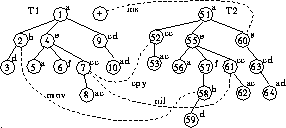
Figure: Annotated edges of the edge cover of
Figure 3
For the above example MH-DIFF produces a minimum-cost edit script, but it may sometimes not find one with globally minimum cost. In Section 6 we evaluate how often this happens and we briefly discuss how one could perform additional searching in the neighborhood of the script found by MH-DIFF.
This concludes the overview of MH-DIFF. To summarize, the process consists of constructing an induced graph from the input trees, pruning the induced graph, finding a minimum-cost edge cover of the pruned induced graph, and finally, using this edge cover to obtain an edit script. In the following sections, we describe these phases in detail. For ease of presentation, we present these phases in a different order than the order in which they are performed. In particular, in Section 4, we begin by formally defining the correspondence between and edit script and an edge cover of the induced graph. In that section, we also describe the method for generating an edit script from an edge cover of the induced graph. In Section 5, we describe how the cost of an edit script is distributed over the edges of the corresponding edge cover of the induced graph. In that section, we also describe how this cost function is approximated by deriving upper and lower bounds on the cost of an edge of the induced graph, and how these bounds are used to prune the induced graph. Since finding a minimum-cost edge cover for a bipartite graph with fixed edge costs is a problem that has been previously studied in the literature [&make_named_href('', "node21.html#combopt","[PS82]"), &make_named_href('', "node21.html#lawler","[Law76]")], we do not present the details in this paper.