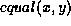 is true if and only if
is true if and only if 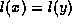 and
and 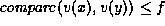 , where f is a parameter valued between 0
and 1. For internal nodes,
, where f is a parameter valued between 0
and 1. For internal nodes, 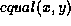 is true if and only
if
is true if and only
if 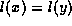 and
and 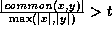 ,
where
,
where 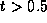 is a parameter.
is a parameter.
Theorem 5.1 allows us to design a simple algorithm for
computing the best matching. This algorithm, called algorithm
Match, is presented in [CRGMW95], and runs in quadratic
time. Below, we present a faster algorithm, called FastMatch,
for computing the unique maximal matching. Our algorithm uses a
function equal to compare nodes. For leaf nodes, 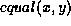 is true if and only if
is true if and only if 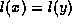 and
and 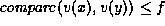 , where f is a parameter valued between 0
and 1. For internal nodes,
, where f is a parameter valued between 0
and 1. For internal nodes, 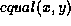 is true if and only
if
is true if and only
if 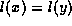 and
and 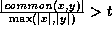 ,
where
,
where 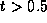 is a parameter.
is a parameter.
Figure 10 shows Algorithm FastMatch, which uses
the longest common subsequence (LCS) routine, introduced earlier in
Section 4.2, to perform an initial matching of
nodes that appear in the same order. Nodes still unmatched after the
call to LCS are processed using linear search. We assume that all
nodes with a given label l in tree T are chained together from
left to right. Let 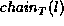 denote the chain of nodes with
label l in tree T. Node x occurs to the left of node y in
denote the chain of nodes with
label l in tree T. Node x occurs to the left of node y in
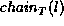 if x appears before y in the in-order traversal
of T when siblings are visited left-to-right.
if x appears before y in the in-order traversal
of T when siblings are visited left-to-right.

Figure 10: Algorithm FastMatch
Now we analyze the running time of Algorithm FastMatch. Define
the weighted edit distance e between trees 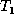 and
and 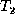 as
follows. Let
as
follows. Let 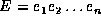 be the shortest edit script that
transforms
be the shortest edit script that
transforms 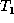 to
to 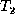 . Then the weighted edit distance is given by
. Then the weighted edit distance is given by
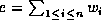 where
where 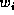 , for
, for 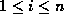 ,
is 1 if
,
is 1 if 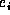 is an insert or a delete, |x| if
is an insert or a delete, |x| if 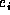 is a move of
the subtree rooted at x, and 0 otherwise. Recall that |x| denotes
the number of leaf nodes that are descendants of node x.
Intuitively, the weighted edit distance indicates how different the
two trees are ``structurally,'' where the degree of difference
associated with the move of a subtree depends on the number of leaves
in the subtree. In [CRGMW95] we show that the running time of
Algorithm FastMatch is proportional to
is a move of
the subtree rooted at x, and 0 otherwise. Recall that |x| denotes
the number of leaf nodes that are descendants of node x.
Intuitively, the weighted edit distance indicates how different the
two trees are ``structurally,'' where the degree of difference
associated with the move of a subtree depends on the number of leaves
in the subtree. In [CRGMW95] we show that the running time of
Algorithm FastMatch is proportional to 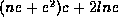 where n is the total number of leaf nodes, c is the average cost
of comparing two leaves (using the compare function), l is
the number of internal node labels, and e is the weighted edit
distance between
where n is the total number of leaf nodes, c is the average cost
of comparing two leaves (using the compare function), l is
the number of internal node labels, and e is the weighted edit
distance between 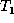 and
and 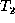 .
.