


Next: The Complete Algorithm
Up: Generating the Edit
Previous: Outline of Algorithm
The align phase of the edit script algorithm presents an interesting
problem. Suppose we detect that for 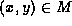 , the children of x
and y are misaligned. In general, there is more than one sequence
of moves that will align the children. For instance, in
Figure 7 there are at least two ways to align the
children of nodes 1 and 11. The first consists of moving nodes 2 and
4 to the right of node 6, and the second consists of moving nodes 3,
5, and 6 to the left of node 2. Both yield the same final
configuration, but the first one is better since it involves
fewer moves.
, the children of x
and y are misaligned. In general, there is more than one sequence
of moves that will align the children. For instance, in
Figure 7 there are at least two ways to align the
children of nodes 1 and 11. The first consists of moving nodes 2 and
4 to the right of node 6, and the second consists of moving nodes 3,
5, and 6 to the left of node 2. Both yield the same final
configuration, but the first one is better since it involves
fewer moves.
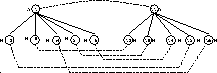
Figure 7: A matching with misaligned nodes
To ensure that the edit script generated by the algorithm is of
minimum cost, we must find the shortest sequence of moves to align the
children of x and y. Our algorithm for finding the shortest
sequence of moves is based on the notion of a longest common
subsequence, described next.
Given a sequence 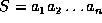 , a sequence
, a sequence 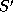 is a
subsequence of S if it can be obtained by deleting zero or more
elements from S. That is,
is a
subsequence of S if it can be obtained by deleting zero or more
elements from S. That is, 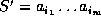 where
where 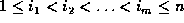 . Given two sequences
. Given two sequences 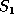 and
and
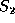 , a longest common subsequence (LCS) of
, a longest common subsequence (LCS) of 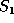 and
and 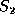 ,
denoted by
,
denoted by 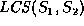 , is a sequence
, is a sequence 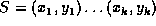 of pairs of elements such that (1)
of pairs of elements such that (1) 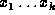 is a
subsequence of
is a
subsequence of 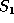 ; (2)
; (2) 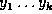 is a subsequence of
is a subsequence of 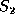 ;
(3) for
;
(3) for 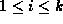 ,
, 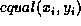 is true for some
predefined equality function equal; and (4) there is no sequence
is true for some
predefined equality function equal; and (4) there is no sequence
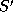 that satisfies conditions 1, 2, and 3 and is longer than S.
The length of an LCS of
that satisfies conditions 1, 2, and 3 and is longer than S.
The length of an LCS of 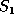 and
and 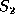 is denoted by
is denoted by 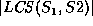 .
.
We use an algorithm due to Myers [Mye86] that computes an LCS of
two sequences in time 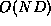 , where
, where 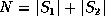 and
and 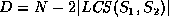 . We treat Myers' LCS algorithm as having three
inputs: the two sequences
. We treat Myers' LCS algorithm as having three
inputs: the two sequences 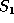 and
and 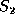 to be compared, and an
equality function
to be compared, and an
equality function 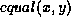 used to compare
used to compare 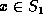 and
and
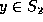 for equality. That is, we treat it as the procedure
for equality. That is, we treat it as the procedure
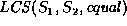 .
.
The solution to the alignment problem is now straightforward. Compute
an LCS S of the matched children of nodes x and y, using the
equality function equal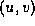 that is true if and only if
that is true if and only if
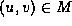 . Leave the children of x that are in S fixed, and
move the remaining matched children of x to the correct positions
relative to the already aligned children. In
Figure 7, the LCS is 3,5,6 (matching the sequence
12,13,14). The moves generated are
. Leave the children of x that are in S fixed, and
move the remaining matched children of x to the correct positions
relative to the already aligned children. In
Figure 7, the LCS is 3,5,6 (matching the sequence
12,13,14). The moves generated are 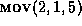 and
and 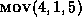 .
In [CRGMW95], we show that our LCS-based strategy always leads
to the minimum number of moves.
.
In [CRGMW95], we show that our LCS-based strategy always leads
to the minimum number of moves.



Next: The Complete Algorithm
Up: Generating the Edit
Previous: Outline of Algorithm
Sudarshan S. Chawathe
Wed Jun 19 08:22:34 PDT 1996
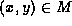 , the children of x
and y are misaligned. In general, there is more than one sequence
of moves that will align the children. For instance, in
Figure 7 there are at least two ways to align the
children of nodes 1 and 11. The first consists of moving nodes 2 and
4 to the right of node 6, and the second consists of moving nodes 3,
5, and 6 to the left of node 2. Both yield the same final
configuration, but the first one is better since it involves
fewer moves.
, the children of x
and y are misaligned. In general, there is more than one sequence
of moves that will align the children. For instance, in
Figure 7 there are at least two ways to align the
children of nodes 1 and 11. The first consists of moving nodes 2 and
4 to the right of node 6, and the second consists of moving nodes 3,
5, and 6 to the left of node 2. Both yield the same final
configuration, but the first one is better since it involves
fewer moves.
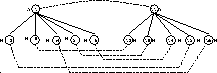
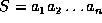 , a sequence
, a sequence 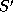 is a
subsequence of S if it can be obtained by deleting zero or more
elements from S. That is,
is a
subsequence of S if it can be obtained by deleting zero or more
elements from S. That is,  where
where 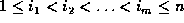 . Given two sequences
. Given two sequences 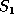 and
and
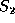 , a longest common subsequence (LCS) of
, a longest common subsequence (LCS) of 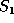 and
and 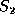 ,
denoted by
,
denoted by 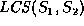 , is a sequence
, is a sequence 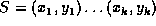 of pairs of elements such that (1)
of pairs of elements such that (1) 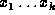 is a
subsequence of
is a
subsequence of 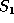 ; (2)
; (2) 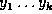 is a subsequence of
is a subsequence of 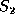 ;
(3) for
;
(3) for 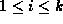 ,
, 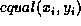 is true for some
predefined equality function equal; and (4) there is no sequence
is true for some
predefined equality function equal; and (4) there is no sequence
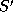 that satisfies conditions 1, 2, and 3 and is longer than S.
The length of an LCS of
that satisfies conditions 1, 2, and 3 and is longer than S.
The length of an LCS of 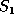 and
and 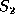 is denoted by
is denoted by 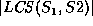 .
.
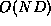 , where
, where 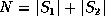 and
and 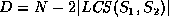 . We treat Myers' LCS algorithm as having three
inputs: the two sequences
. We treat Myers' LCS algorithm as having three
inputs: the two sequences 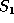 and
and 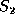 to be compared, and an
equality function
to be compared, and an
equality function 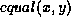 used to compare
used to compare 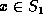 and
and
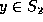 for equality. That is, we treat it as the procedure
for equality. That is, we treat it as the procedure
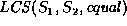 .
.
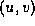 that is true if and only if
that is true if and only if
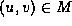 . Leave the children of x that are in S fixed, and
move the remaining matched children of x to the correct positions
relative to the already aligned children. In
Figure
. Leave the children of x that are in S fixed, and
move the remaining matched children of x to the correct positions
relative to the already aligned children. In
Figure 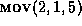 and
and 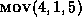 .
In [
.
In [