


Next: Finding Good Matchings
Up: Generating the Edit
Previous: Aligning Children
We now present the complete algorithm to compute a minimum cost edit
script E conforming to a given matching M between trees 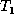 and
and
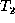 . In the algorithm, we combine the first four phases of
Section 4.1 (the update, insert, align, and move phases)
into one breadth-first scan on
. In the algorithm, we combine the first four phases of
Section 4.1 (the update, insert, align, and move phases)
into one breadth-first scan on 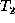 . The delete phase requires a
post-order traversal of
. The delete phase requires a
post-order traversal of 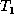 (which visits each node after visiting
all its children). The order in which the nodes are visited and the
edit operations are generated is crucial to the correctness of the
algorithm. (For example, an insert may need to precede a move, if the
moved node becomes the child of the inserted node.) The algorithm
applies the edit operations to
(which visits each node after visiting
all its children). The order in which the nodes are visited and the
edit operations are generated is crucial to the correctness of the
algorithm. (For example, an insert may need to precede a move, if the
moved node becomes the child of the inserted node.) The algorithm
applies the edit operations to 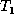 as they are appended to the edit
script E. When the algorithm terminates,
as they are appended to the edit
script E. When the algorithm terminates, 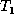 is isomorphic to
is isomorphic to
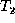 . The algorithm also uses a matching
. The algorithm also uses a matching 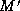 that is initially M,
and adds matches to it so that
that is initially M,
and adds matches to it so that 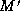 is a total matching when the
algorithm terminates. As mentioned earlier, we assume without loss of
generality that the roots of
is a total matching when the
algorithm terminates. As mentioned earlier, we assume without loss of
generality that the roots of 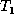 and
and 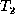 are matched in M.
are matched in M.

Figure 8: Algorithm EditScript
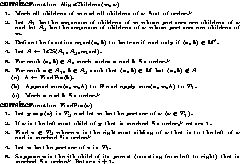
Figure 9: Functions AlignChildren and FindPos
The algorithm is shown in Figure 8. It uses two
procedures, AlignChildren and FindPos, shown in
Figure 9. The claims made by the two
statements in Algorithm EditScript that are marked with (*)
are substantiated in [CRGMW95], where it is also proved that
Algorithm EditScript generates a minimum cost edit script
conforming to the given matching M.
Let us now consider the running time of this algorithm. We first
define the notion of misaligned nodes. Suppose 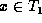 and
and
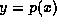 . A move of the form
. A move of the form 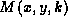 for some k is called an
intra-parent move of node x; such moves are generated in the
align phase of the algorithm. The number of misaligned nodes of
for some k is called an
intra-parent move of node x; such moves are generated in the
align phase of the algorithm. The number of misaligned nodes of 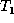 with respect to
with respect to 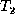 is the minimum number of intra-parent moves
among all minimum cost edit scripts. We can show [CRGMW95]
that the running time of Algorithm EditScript is
is the minimum number of intra-parent moves
among all minimum cost edit scripts. We can show [CRGMW95]
that the running time of Algorithm EditScript is 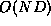 ,
where N is the total number of nodes in
,
where N is the total number of nodes in 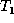 and
and 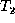 and D is
the total number of misaligned nodes. (Note that D is typically
much smaller than N.)
and D is
the total number of misaligned nodes. (Note that D is typically
much smaller than N.)



Next: Finding Good Matchings
Up: Generating the Edit
Previous: Aligning Children
Sudarshan S. Chawathe
Wed Jun 19 08:22:34 PDT 1996
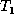 and
and
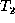 . In the algorithm, we combine the first four phases of
Section 4.1 (the update, insert, align, and move phases)
into one breadth-first scan on
. In the algorithm, we combine the first four phases of
Section 4.1 (the update, insert, align, and move phases)
into one breadth-first scan on 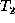 . The delete phase requires a
post-order traversal of
. The delete phase requires a
post-order traversal of 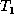 (which visits each node after visiting
all its children). The order in which the nodes are visited and the
edit operations are generated is crucial to the correctness of the
algorithm. (For example, an insert may need to precede a move, if the
moved node becomes the child of the inserted node.) The algorithm
applies the edit operations to
(which visits each node after visiting
all its children). The order in which the nodes are visited and the
edit operations are generated is crucial to the correctness of the
algorithm. (For example, an insert may need to precede a move, if the
moved node becomes the child of the inserted node.) The algorithm
applies the edit operations to 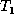 as they are appended to the edit
script E. When the algorithm terminates,
as they are appended to the edit
script E. When the algorithm terminates, 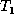 is isomorphic to
is isomorphic to
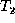 . The algorithm also uses a matching
. The algorithm also uses a matching 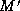 that is initially M,
and adds matches to it so that
that is initially M,
and adds matches to it so that 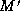 is a total matching when the
algorithm terminates. As mentioned earlier, we assume without loss of
generality that the roots of
is a total matching when the
algorithm terminates. As mentioned earlier, we assume without loss of
generality that the roots of 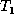 and
and 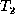 are matched in M.
are matched in M.

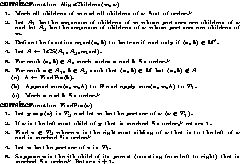
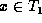 and
and
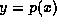 . A move of the form
. A move of the form 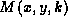 for some k is called an
intra-parent move of node x; such moves are generated in the
align phase of the algorithm. The number of misaligned nodes of
for some k is called an
intra-parent move of node x; such moves are generated in the
align phase of the algorithm. The number of misaligned nodes of 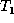 with respect to
with respect to 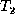 is the minimum number of intra-parent moves
among all minimum cost edit scripts. We can show [
is the minimum number of intra-parent moves
among all minimum cost edit scripts. We can show [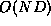 ,
where N is the total number of nodes in
,
where N is the total number of nodes in 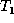 and
and 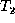 and D is
the total number of misaligned nodes. (Note that D is typically
much smaller than N.)
and D is
the total number of misaligned nodes. (Note that D is typically
much smaller than N.)