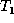 into
into 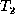 , given the matching M
shown by the dashed lines in the figure.
, given the matching M
shown by the dashed lines in the figure.
The algorithm is most easily explained as consisting of the five
phases that we describe below. We use our running example from
Figure 1. We are required to find a minimum cost
edit script that transforms 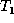 into
into 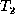 , given the matching M
shown by the dashed lines in the figure.
, given the matching M
shown by the dashed lines in the figure.
The Update Phase:
In the update phase, we look for pairs of nodes 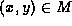 such
that the values at nodes x and y differ. For each such pair (in
any order) we add the edit operation
such
that the values at nodes x and y differ. For each such pair (in
any order) we add the edit operation 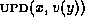 to E (recall
that for a node x,
to E (recall
that for a node x, 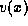 denotes the value of x), and we apply
the update operation to
denotes the value of x), and we apply
the update operation to 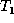 . At the end of the update phase, we have
transformed
. At the end of the update phase, we have
transformed 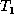 such that
such that 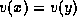 for every pair of nodes
for every pair of nodes
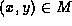 .
.
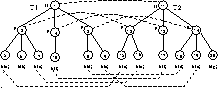
Figure 4: Running example: after align phase
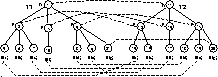
Figure 5: Running example: after insert phase
The Align Phase: Let the partner of a node denote the
node to which it is matched (by a given matching). Suppose 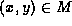 . We say that the children of x and y are misaligned if
x has matched children u and v such that u is to the left of
v in
. We say that the children of x and y are misaligned if
x has matched children u and v such that u is to the left of
v in 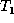 but the partner of u is to the right of the partner of
v in
but the partner of u is to the right of the partner of
v in 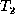 . In Figure 1, the children of the root
nodes 1 and 11 are misaligned. In the align phase we check each pair
of matched internal nodes
. In Figure 1, the children of the root
nodes 1 and 11 are misaligned. In the align phase we check each pair
of matched internal nodes 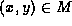 (in any order) to see if their
children are misaligned. If we find that the children are misaligned,
we append move operations to E to align the children. We explain
how the move operations are determined in
Section 4.2 below. In our running example, we
append
(in any order) to see if their
children are misaligned. If we find that the children are misaligned,
we append move operations to E to align the children. We explain
how the move operations are determined in
Section 4.2 below. In our running example, we
append 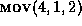 to E, and we apply the move operation to
to E, and we apply the move operation to 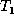 .
The new
.
The new 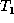 is shown in Figure 4.
is shown in Figure 4.
The Insert Phase: We assume, without loss of generality, that
the roots of 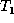 and
and 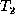 are matched in M.
are matched in M.![]() In the insert phase, we look for an unmatched node
In the insert phase, we look for an unmatched node
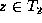 such that its parent is matched. Suppose
such that its parent is matched. Suppose 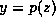 (i.e., y is the parent of z) and y's partner in
(i.e., y is the parent of z) and y's partner in 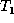 is x.
We create a new identifier w and append
is x.
We create a new identifier w and append 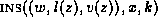 to
E. The position k is determined with respect to the children of
x and z that have already been aligned with respect to each other;
details are in Section 4.3. We also apply the
insert operation to
to
E. The position k is determined with respect to the children of
x and z that have already been aligned with respect to each other;
details are in Section 4.3. We also apply the
insert operation to 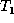 and add
and add 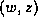 to M. In our running
example we append
to M. In our running
example we append 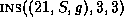 . The transformed
. The transformed 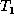 and the
augmented M are shown in Figure 5. At the end of
the insert phase, every node in
and the
augmented M are shown in Figure 5. At the end of
the insert phase, every node in 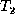 is matched but there may still
be nodes in
is matched but there may still
be nodes in 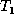 that are unmatched.
that are unmatched.
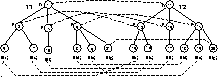
Figure 6: Running example: after delete phase
The Move Phase: In the move phase we look for pairs of nodes
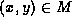 such that
such that 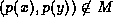 . (Recall from
Section 3.1 that
. (Recall from
Section 3.1 that 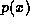 denotes the parent of x.)
Suppose
denotes the parent of x.)
Suppose 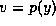 . We know that at the end of the insert phase, v
has some partner u in
. We know that at the end of the insert phase, v
has some partner u in 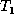 . We append the operation
. We append the operation 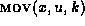 to E, and we apply the move operation to
to E, and we apply the move operation to 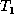 . Here the position
k is determined with respect to the children of u and v that
have already been aligned, as in the insert phase. At the end of the
move phase
. Here the position
k is determined with respect to the children of u and v that
have already been aligned, as in the insert phase. At the end of the
move phase 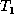 is isomorphic to
is isomorphic to 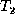 except for unmatched nodes in
except for unmatched nodes in
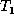 . In our running example, we do not need to perform any actions
in this phase.
. In our running example, we do not need to perform any actions
in this phase.
The Delete Phase:
In the delete phase we look for unmatched leaf nodes 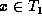 . For
each such node we append
. For
each such node we append 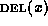 to E and apply the delete
operation to
to E and apply the delete
operation to 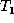 . (Note that this process will result in a bottom-up
delete---descendents will be deleted before their ancestors.) At the
end of the delete phase
. (Note that this process will result in a bottom-up
delete---descendents will be deleted before their ancestors.) At the
end of the delete phase 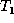 is isomorphic to
is isomorphic to 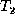 , E is the final
edit script, and M is the total matching to which E conforms.
Figure 6 shows the trees and the matching after the
delete phase.
, E is the final
edit script, and M is the total matching to which E conforms.
Figure 6 shows the trees and the matching after the
delete phase.