


Next: Summary and Future
Up: Implementation and Performance
Previous: Empirical Evaluation of
Another issue that needs to be addressed is the effect of
Assumption 2 on the quality of the solution produced by
FastMatch. Recall from Section 5 that FastMatch is
guaranteed to produce an optimal matching only when
Assumption 2 holds. When Assumption 2 does
not hold, the algorithm may produce a suboptimal matching. We
describe a post-processing step that, when added to FastMatch, enables
us to convert the possibly suboptimal matching produced by FastMatch
into an optimal one in many cases: Proceeding top-down, we consider
each tree node x in turn. Let y be the partner of x according to
the current matching. For each child c of x that is matched to a
node 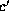 such that
such that 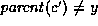 , we check
if we can match c to a child
, we check
if we can match c to a child 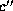 of y, such that
of y, such that
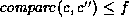 , where f is the
parameter used in Matching Criterion 1. If so, we change the
current matching to make c match
, where f is the
parameter used in Matching Criterion 1. If so, we change the
current matching to make c match 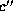 . This
post-processing phase removes some of the suboptimalities that may be
introduced if Assumption 2 does not hold for all
nodes.
. This
post-processing phase removes some of the suboptimalities that may be
introduced if Assumption 2 does not hold for all
nodes.
Even with post-processing, it is still possible to have a suboptimal
solution, as follows: Recall that FastMatch begins by matching leaves,
and then proceeds to match higher levels in the tree in a bottom-up
manner. With this approach, a mismatch at a lower level may
``propagate,'' causing a mismatch at one or more higher levels. Our
post-processing step will correct all mismatches other than those that
propagated from lower levels to higher levels. It is difficult to
evaluate precisely those cases that in which this propagation occurs
without performing exhaustive computations. However, we can derive a
necessary (but not sufficient) condition for propagation, and then
measure that condition in our experiments. Informally, this condition
states that in order to be mismatched, a node must have more than a
certain number of children that violate Assumption 2,
where the exact number depends on the match threshold t. Actually,
this condition is weak; a node must satisfy many other conditions for
the possibility of a mismatch to exist, and even then a mismatch is
not guaranteed.
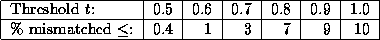
Table 1: Mismatched paragraphs in FastMatch.
For the same document data analyzed earlier, Table 1
shows some statistics on the percentage of paragraphs that may
be mismatched for a given value of the match threshold t. For
example, we see that with 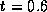 , we may mismatch at most 1% of the
paragraphs. A lower value of t results in a lower number of
possible mismatches. We see that the number of mismatched paragraphs
is low, supporting our claim. Since the condition used to determine
when a mismatch may occur is a weak one, the percentage of mismatches
is expected to be much lower than suggested by these numbers.
Furthermore, note that a suboptimal matching compromises only the
quality of an edit script produced as the final output, not its
correctness. In many applications, this trade-off between optimality
and efficiency is a reasonable one. For example, when computing the
delta between two documents, it is often not critical if the edit
script produced is slightly longer than the optimal one.
, we may mismatch at most 1% of the
paragraphs. A lower value of t results in a lower number of
possible mismatches. We see that the number of mismatched paragraphs
is low, supporting our claim. Since the condition used to determine
when a mismatch may occur is a weak one, the percentage of mismatches
is expected to be much lower than suggested by these numbers.
Furthermore, note that a suboptimal matching compromises only the
quality of an edit script produced as the final output, not its
correctness. In many applications, this trade-off between optimality
and efficiency is a reasonable one. For example, when computing the
delta between two documents, it is often not critical if the edit
script produced is slightly longer than the optimal one.



Next: Summary and Future
Up: Implementation and Performance
Previous: Empirical Evaluation of
Sudarshan S. Chawathe
Wed Jun 19 08:22:34 PDT 1996
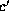 such that
such that 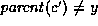 , we check
if we can match c to a child
, we check
if we can match c to a child 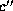 of y, such that
of y, such that
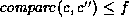 , where f is the
parameter used in Matching Criterion 1. If so, we change the
current matching to make c match
, where f is the
parameter used in Matching Criterion 1. If so, we change the
current matching to make c match 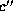 . This
post-processing phase removes some of the suboptimalities that may be
introduced if Assumption 2 does not hold for all
nodes.
. This
post-processing phase removes some of the suboptimalities that may be
introduced if Assumption 2 does not hold for all
nodes.
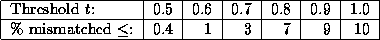
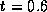 , we may mismatch at most 1% of the
paragraphs. A lower value of t results in a lower number of
possible mismatches. We see that the number of mismatched paragraphs
is low, supporting our claim. Since the condition used to determine
when a mismatch may occur is a weak one, the percentage of mismatches
is expected to be much lower than suggested by these numbers.
Furthermore, note that a suboptimal matching compromises only the
quality of an edit script produced as the final output, not its
correctness. In many applications, this trade-off between optimality
and efficiency is a reasonable one. For example, when computing the
delta between two documents, it is often not critical if the edit
script produced is slightly longer than the optimal one.
, we may mismatch at most 1% of the
paragraphs. A lower value of t results in a lower number of
possible mismatches. We see that the number of mismatched paragraphs
is low, supporting our claim. Since the condition used to determine
when a mismatch may occur is a weak one, the percentage of mismatches
is expected to be much lower than suggested by these numbers.
Furthermore, note that a suboptimal matching compromises only the
quality of an edit script produced as the final output, not its
correctness. In many applications, this trade-off between optimality
and efficiency is a reasonable one. For example, when computing the
delta between two documents, it is often not critical if the edit
script produced is slightly longer than the optimal one.