


Next: Quality of FastMatch's
Up: Implementation and Performance
Previous: Implementation
Recall from Section 5 that the running time of
Algorithm FastMatch is given by an expression of the form 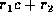 . In this expression,
. In this expression, 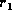 represents the number of
leaf node comparisons (invocations of function compare), c is
the average cost of comparing leaf nodes, and
represents the number of
leaf node comparisons (invocations of function compare), c is
the average cost of comparing leaf nodes, and 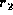 represents the
number of node partner checks. Partner checks are implemented in
LaDiff as integer comparisons. We know that
represents the
number of node partner checks. Partner checks are implemented in
LaDiff as integer comparisons. We know that 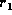 is bounded by
is bounded by 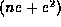 , and that
, and that 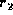 is bounded by 2lne , where n is the
number of tree nodes, e is the weighted edit distance between the
two trees, and l is the number of internal node labels. The
parameter e depends on the nature of the differences between the
trees (recall the definition of weighted edit distance in Section
5.2).
is bounded by 2lne , where n is the
number of tree nodes, e is the weighted edit distance between the
two trees, and l is the number of internal node labels. The
parameter e depends on the nature of the differences between the
trees (recall the definition of weighted edit distance in Section
5.2).
There are two reasons for studying the performance of FastMatch
empirically. The first reason is that the formula for the running
time contains the weighted edit distance, e, which is difficult to
estimate in terms of the input. A more natural measure of the input
size is the number of edit operations in an optimal edit script, which
we call the unweighted edit distance, d. We can show
analytically that the ratio 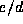 is bounded by
is bounded by 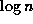 for a large
class of inputs, but we believe that in real cases, its value is much
lower than
for a large
class of inputs, but we believe that in real cases, its value is much
lower than 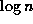 . We therefore study the relationship between e
and d empirically. The second reason is that we would like to test
our conjecture that the analytical bound on the running time of
FastMatch is ``loose,'' and in most practical situations the algorithm
runs much faster.
. We therefore study the relationship between e
and d empirically. The second reason is that we would like to test
our conjecture that the analytical bound on the running time of
FastMatch is ``loose,'' and in most practical situations the algorithm
runs much faster.
Figure 11: Weighted edit distance
For our performance study, we used three sets of files. The files in
each set represent different versions of a document (a conference
paper). We ran FastMatch on pairs of files within each of these three
sets. (Comparing files across sets is not meaningful because we would
be comparing two completely different documents.) In
Figure 11 we indicate how the weighted edit distance
(e) varies with the unweighted edit distance (d), for each of the
three document sets. Recall that n is the number of tree leaves,
that is, the number of sentences in the document. We see that the
relationship between e and d is close to linear. Furthermore,
the variance with respect to the three document sets is not high,
suggesting that 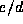 is not very sensitive to the size of the
documents (n). The average value of
is not very sensitive to the size of the
documents (n). The average value of 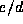 is 3.4 for these
documents.
is 3.4 for these
documents.
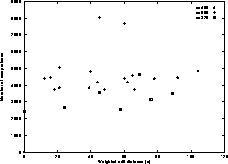
Figure 12: Running time
In Figure 12 we plot how the running time of
FastMatch varies with the weighted edit distance e. The vertical
axis is the running time as measured by the number of comparisons made
by FastMatch and the horizontal axis is the weighted edit distance.
Note that the analytical bound on the number of comparisons made by
FastMatch is much higher than the numbers depicted in
Figure 12; on the average, FastMatch makes
approximately 20 times fewer comparisons than those predicted by the
analytical bound, supporting our conjecture that the analytical
bound on the running time is a loose one. We also observe that
Figure 12 suggests an approximately linear relation
between the running time and e, although there is a high variance.
This variance may be explained by our first observation that the
actual running time is far below the predicted bound.



Next: Quality of FastMatch's
Up: Implementation and Performance
Previous: Implementation
Sudarshan S. Chawathe
Wed Jun 19 08:22:34 PDT 1996
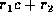 . In this expression,
. In this expression, 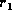 represents the number of
leaf node comparisons (invocations of function compare), c is
the average cost of comparing leaf nodes, and
represents the number of
leaf node comparisons (invocations of function compare), c is
the average cost of comparing leaf nodes, and 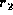 represents the
number of node partner checks. Partner checks are implemented in
LaDiff as integer comparisons. We know that
represents the
number of node partner checks. Partner checks are implemented in
LaDiff as integer comparisons. We know that 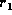 is bounded by
is bounded by 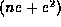 , and that
, and that 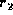 is bounded by 2lne , where n is the
number of tree nodes, e is the weighted edit distance between the
two trees, and l is the number of internal node labels. The
parameter e depends on the nature of the differences between the
trees (recall the definition of weighted edit distance in Section
5.2).
is bounded by 2lne , where n is the
number of tree nodes, e is the weighted edit distance between the
two trees, and l is the number of internal node labels. The
parameter e depends on the nature of the differences between the
trees (recall the definition of weighted edit distance in Section
5.2).
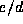 is bounded by
is bounded by 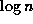 for a large
class of inputs, but we believe that in real cases, its value is much
lower than
for a large
class of inputs, but we believe that in real cases, its value is much
lower than 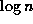 . We therefore study the relationship between e
and d empirically. The second reason is that we would like to test
our conjecture that the analytical bound on the running time of
FastMatch is ``loose,'' and in most practical situations the algorithm
runs much faster.
. We therefore study the relationship between e
and d empirically. The second reason is that we would like to test
our conjecture that the analytical bound on the running time of
FastMatch is ``loose,'' and in most practical situations the algorithm
runs much faster.

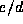 is not very sensitive to the size of the
documents (n). The average value of
is not very sensitive to the size of the
documents (n). The average value of 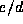 is 3.4 for these
documents.
is 3.4 for these
documents.
